jblc
Mechanical
- Apr 2, 2009
- 24
This questions related to feedforward (FF) and feedback (FB) interactions.
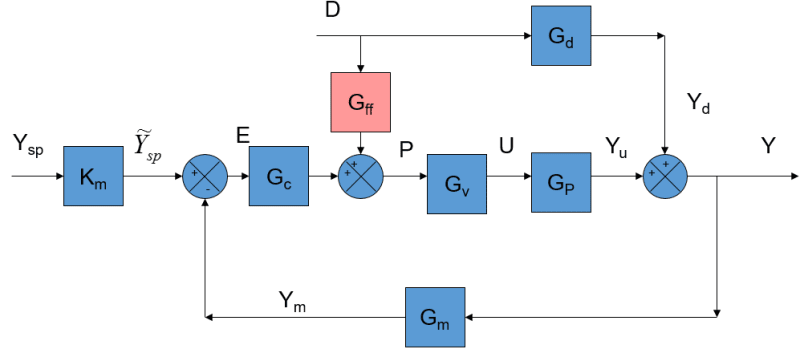
Say there's a system who's goal is to keep a car centered in a lane. Say it includes a FF sensor (like detecting sideways wind hitting the car, or an inclinometer to detect the sideways slope of the road), and a FB sensor (like finding the lane markings)
1) Running FF by itself works fine.
Running a FB loop by itself works fine.
When combining them, i would have thought the performance due to combined efforts would be BETTER than either one by itself.
But, what i'm seeing is the exact same performance when FF is run along with FB, as when only FB is run by itself:
- when FF is activated, the FB loop command signal is reduced by the same amount that the FF has contributed. Ie, FB sees a smaller error, and so the performance ends up the same.
- And vice versa: when FF is deactivated, FB quickly fills the gap left by FF.
2) Seemingly, there should be a specific relation needed between the dynamics of FF and the FB loop, ie FF is effective when FB is physically not capable of responding fast enough due to it sensor or loop dynamics, etc., and so FF is needed to fill that gap.
But even in the case with similar dynamics, say a case with suboptimal FB loop tuning, i would have thought that adding FF would strictly improve performance.
Question: In the case that the FF and FB have similar dynamics, how can I set up FB in a way that it DOES NOT take into account the FF's positive impact, so that the combined behavior is higher performance? Ie, so that FB acts with the same commands to the plant, as if FF were inactive.
Naively, one method seems like it'd involve backing out the impact of the FF (ie how the plant would respond to the FF command), and adding that back to the FB loop's error. This seems highly error-proned though, and i'm sure there are many official methods for this...
Say there's a system who's goal is to keep a car centered in a lane. Say it includes a FF sensor (like detecting sideways wind hitting the car, or an inclinometer to detect the sideways slope of the road), and a FB sensor (like finding the lane markings)
1) Running FF by itself works fine.
Running a FB loop by itself works fine.
When combining them, i would have thought the performance due to combined efforts would be BETTER than either one by itself.
But, what i'm seeing is the exact same performance when FF is run along with FB, as when only FB is run by itself:
- when FF is activated, the FB loop command signal is reduced by the same amount that the FF has contributed. Ie, FB sees a smaller error, and so the performance ends up the same.
- And vice versa: when FF is deactivated, FB quickly fills the gap left by FF.
2) Seemingly, there should be a specific relation needed between the dynamics of FF and the FB loop, ie FF is effective when FB is physically not capable of responding fast enough due to it sensor or loop dynamics, etc., and so FF is needed to fill that gap.
But even in the case with similar dynamics, say a case with suboptimal FB loop tuning, i would have thought that adding FF would strictly improve performance.
Question: In the case that the FF and FB have similar dynamics, how can I set up FB in a way that it DOES NOT take into account the FF's positive impact, so that the combined behavior is higher performance? Ie, so that FB acts with the same commands to the plant, as if FF were inactive.
Naively, one method seems like it'd involve backing out the impact of the FF (ie how the plant would respond to the FF command), and adding that back to the FB loop's error. This seems highly error-proned though, and i'm sure there are many official methods for this...