MelBWasHere
Structural
I have a 50ksi wide flange beam that I'm reinforcing with a 50ksi WT (welding the stem to the bottom flange of the wide flange).
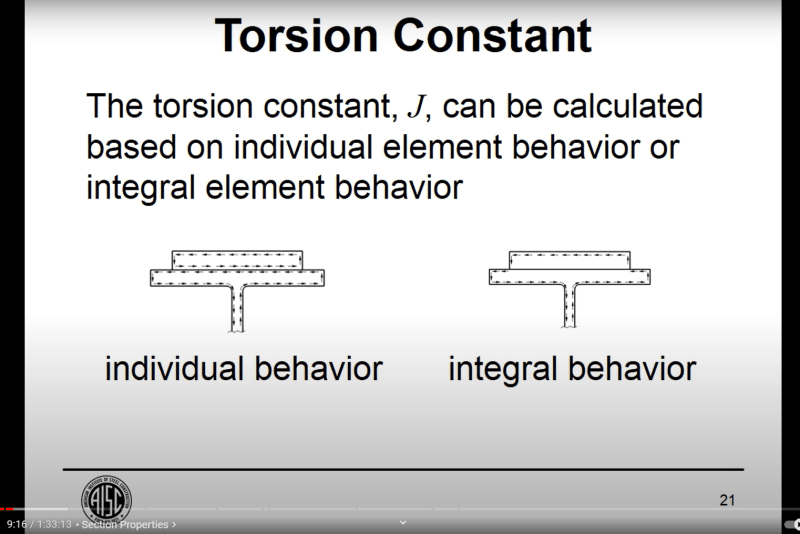
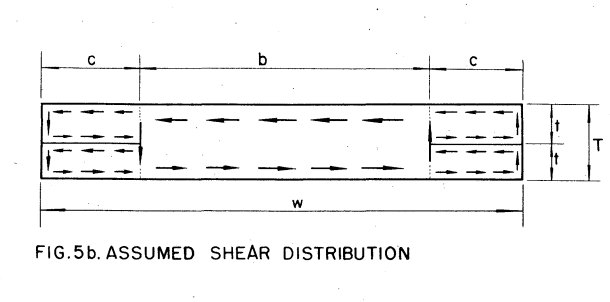
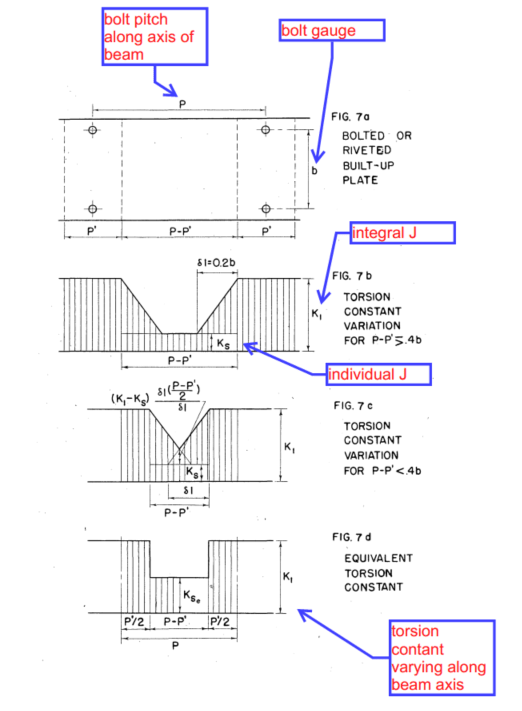
I'm trying to check the LTB limit state of the member per AISC 360-16 Section F4.2, but am having trouble figuring out how to calculate the torsional constant, J.
I don't trust software, since every one that I've used has given me different answers for all section properties (varying by 2-4%, which I'm wary to accept), so I'd like to figure out how to do this by hand.
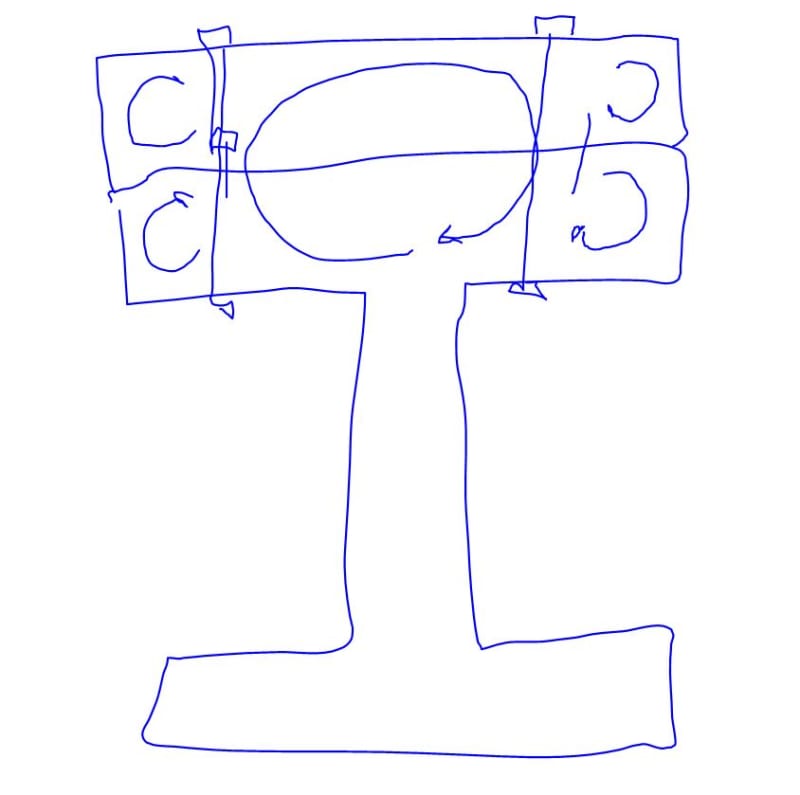
Would it be conservative to assume the torsional constants are additive?
I'm trying to check the LTB limit state of the member per AISC 360-16 Section F4.2, but am having trouble figuring out how to calculate the torsional constant, J.
I don't trust software, since every one that I've used has given me different answers for all section properties (varying by 2-4%, which I'm wary to accept), so I'd like to figure out how to do this by hand.
Would it be conservative to assume the torsional constants are additive?