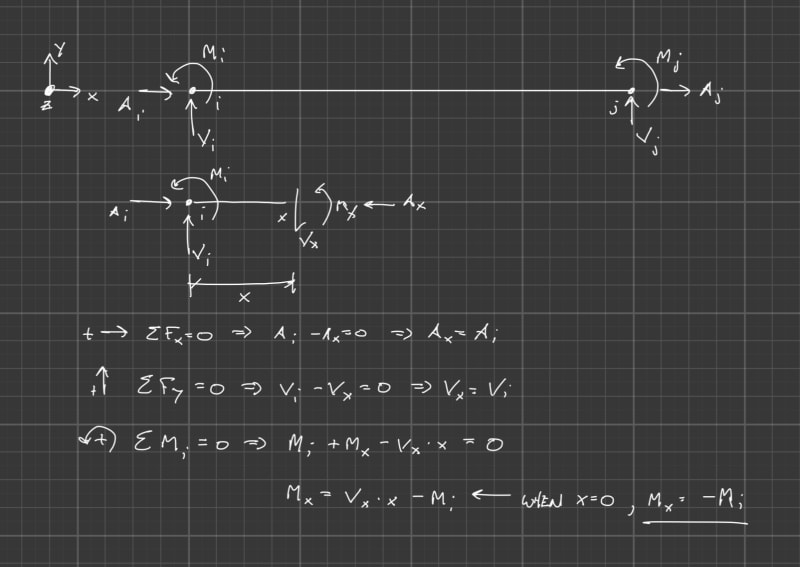Tygra_1983
Student
Hi there,
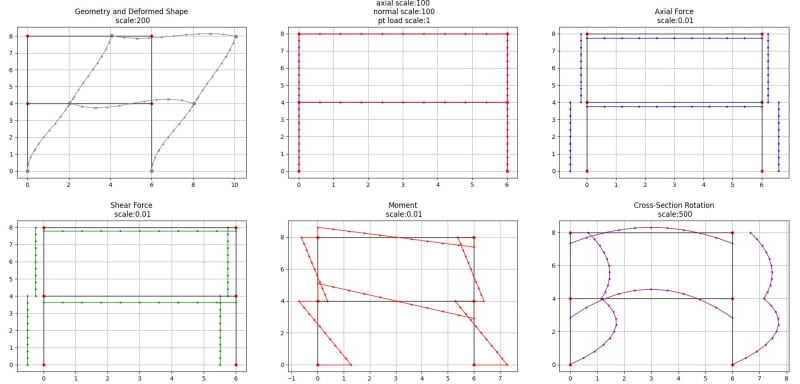
I was wondering if someone might know why I am getting incorrect signs for my structure that I am working on using the Direct Stiffness Method? I am following the procedure that I was taught when I was at University and I can't completely remember everything. I am designing a seven-storey structure that looks like this:
The magnitude of the forces I am getting is accurate, but the signs are incorrect.
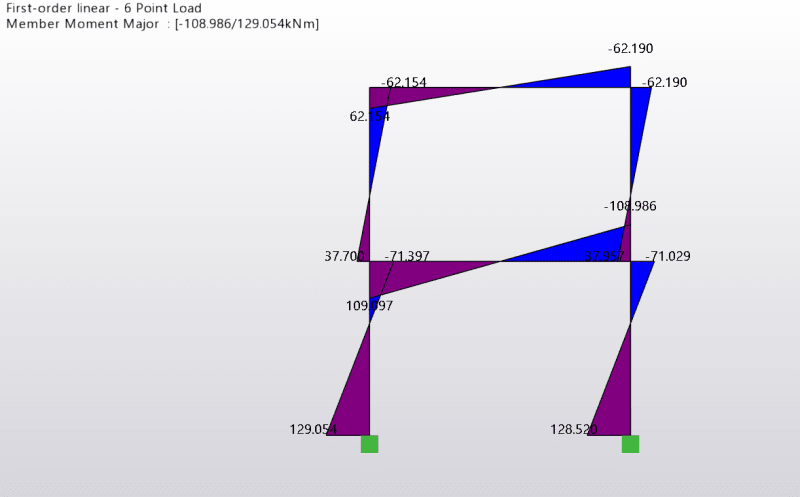
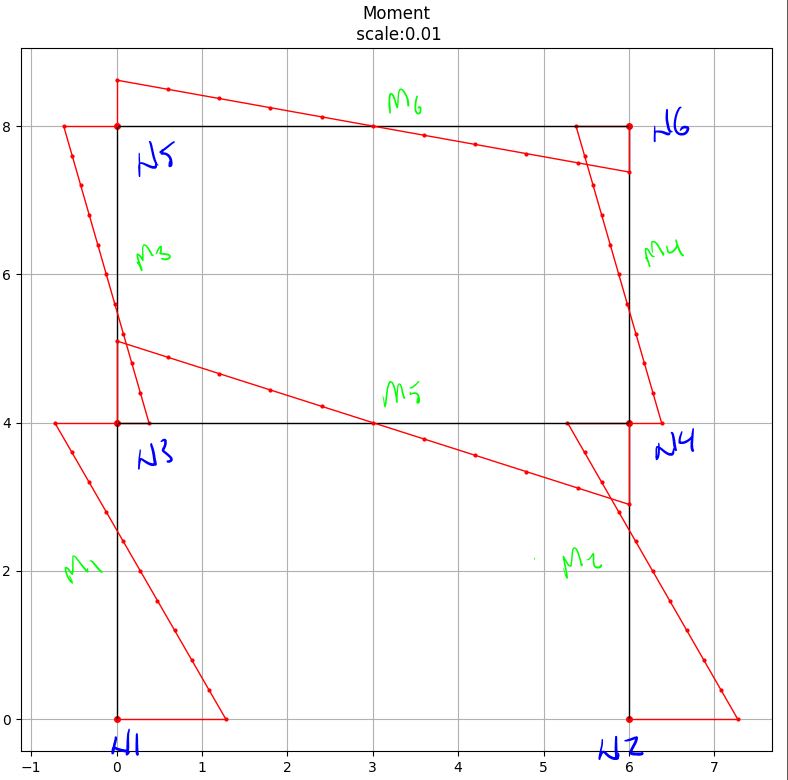
Here are the bending moment on the structure:
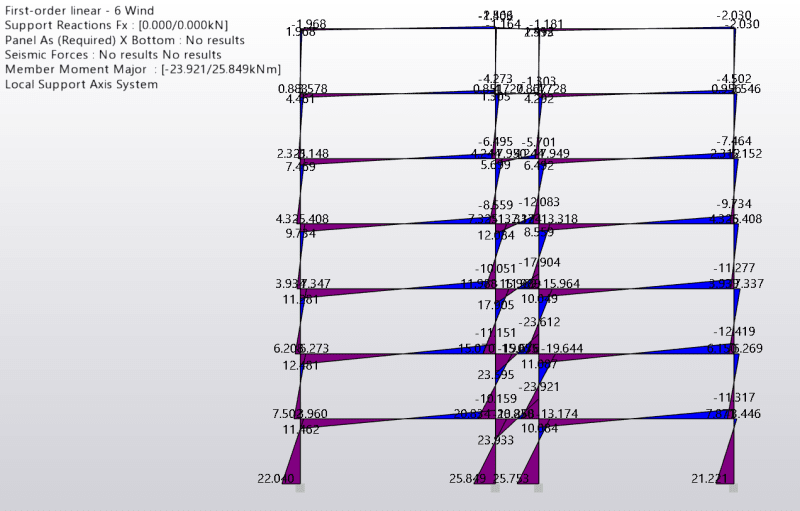
You might not be able to see, but for the columns, you get a positive bending moment at the bottom of each storey and a negative bending moment at the top of the storey - this pattern is the same for each storey.
In my code I am getting positive bending moments at the top and the bottom, but like I said the magnitude is quite accurate.
Rather than post the entirity of my code, lets focus on a single column.
The local stiffness matrix for a column has the form:
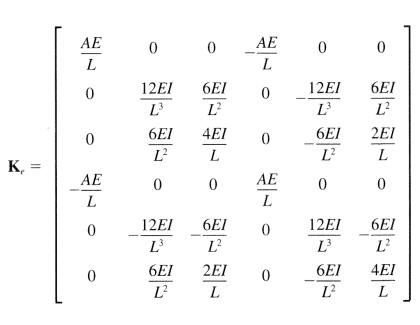
And I set up the transformation matrix as follows:
Code:
To compute the global stiffness matrix you use the equation:
Kglobal = T(transpose)*KLocal*T
This will give you the global stiffness matrix! You can then proceed to find the displacements and rotations. Then you can find the internal forces on the structure.
I guess the thing to look at is the transformation matrix. Does it seem correct to you? The local stiffness matrix is definitely correct.
Many thanks in advance
I was wondering if someone might know why I am getting incorrect signs for my structure that I am working on using the Direct Stiffness Method? I am following the procedure that I was taught when I was at University and I can't completely remember everything. I am designing a seven-storey structure that looks like this:

The magnitude of the forces I am getting is accurate, but the signs are incorrect.
Here are the bending moment on the structure:

You might not be able to see, but for the columns, you get a positive bending moment at the bottom of each storey and a negative bending moment at the top of the storey - this pattern is the same for each storey.
In my code I am getting positive bending moments at the top and the bottom, but like I said the magnitude is quite accurate.
Rather than post the entirity of my code, lets focus on a single column.
The local stiffness matrix for a column has the form:
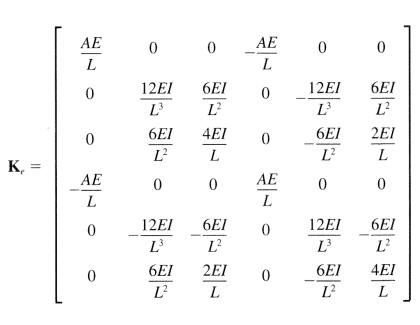
And I set up the transformation matrix as follows:
Code:
Code:
T =
6x6 table
U1 V1 theta1 U2 V2 theta2
__ __ ______ __ __ ______
U1 0 1 0 0 0 0
V1 -1 0 0 0 0 0
theta1 0 0 1 0 0 0
U2 0 0 0 0 1 0
V2 0 0 0 -1 0 0
theta2 0 0 0 0 0 1To compute the global stiffness matrix you use the equation:
Kglobal = T(transpose)*KLocal*T
This will give you the global stiffness matrix! You can then proceed to find the displacements and rotations. Then you can find the internal forces on the structure.
I guess the thing to look at is the transformation matrix. Does it seem correct to you? The local stiffness matrix is definitely correct.
Many thanks in advance