Hello everyone! I'm studying for an exam and I was practicing op-amps. This specific one popped up at one of my professor's exams but I'm very unsure as to how I'm supposed to proceed.
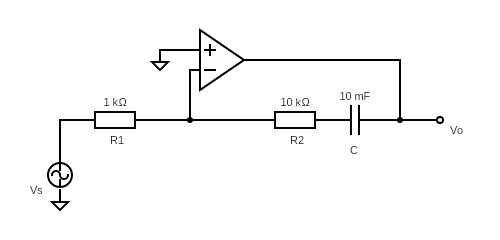
Besides the values the resistors and capacitor in the picture, I know that AOL = 74dB and Zout = 5 ohms.
I'm supposed to find an expression for the transfer function, plot the Bode diagram and calculate mid-band gain. Normally if I were given an op-amp with ideally infinite open loop gain I'd just use the virtual short method to calculate the transfer function, or even just divide the feedback impedance by the input impedance (in this case, (R1 + R2 + ZC)/R1 however the open loop gain and output impedance threw me off. I'm assuming that they both have an effect on the transfer function, so I was thinking of working my way to it using AV = (AOL/(1 + βAOL). In this case, feedback factor β would be (R1/(R1 + R2 + ZC). Replacing ZC with 1/sC this is the expression for β that I got:
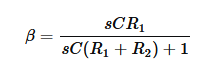
And plugging it into AV = (AOL/(1 + βAOL) this is what I ended up with, kinda got messy but it should be correct (not sure if it is)
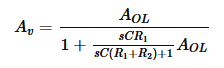
rearranged:
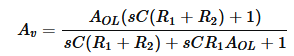
Now, I was wondering if my approach up until here is correct, and which one is. Is the last expression for Av, the one that takes in consideration AOL correct, or am I just supposed to get an expression for the transfer function with VO/VS = -ZF/ZIN (ZF being the impedance in the feedback network).
Thank you very much!

Besides the values the resistors and capacitor in the picture, I know that AOL = 74dB and Zout = 5 ohms.
I'm supposed to find an expression for the transfer function, plot the Bode diagram and calculate mid-band gain. Normally if I were given an op-amp with ideally infinite open loop gain I'd just use the virtual short method to calculate the transfer function, or even just divide the feedback impedance by the input impedance (in this case, (R1 + R2 + ZC)/R1 however the open loop gain and output impedance threw me off. I'm assuming that they both have an effect on the transfer function, so I was thinking of working my way to it using AV = (AOL/(1 + βAOL). In this case, feedback factor β would be (R1/(R1 + R2 + ZC). Replacing ZC with 1/sC this is the expression for β that I got:
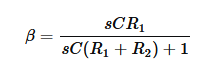
And plugging it into AV = (AOL/(1 + βAOL) this is what I ended up with, kinda got messy but it should be correct (not sure if it is)
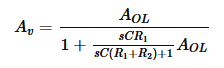
rearranged:
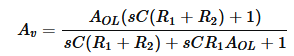
Now, I was wondering if my approach up until here is correct, and which one is. Is the last expression for Av, the one that takes in consideration AOL correct, or am I just supposed to get an expression for the transfer function with VO/VS = -ZF/ZIN (ZF being the impedance in the feedback network).
Thank you very much!
