-
1
- #1
weavedreamer
Automotive
- Aug 1, 2007
- 279
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.

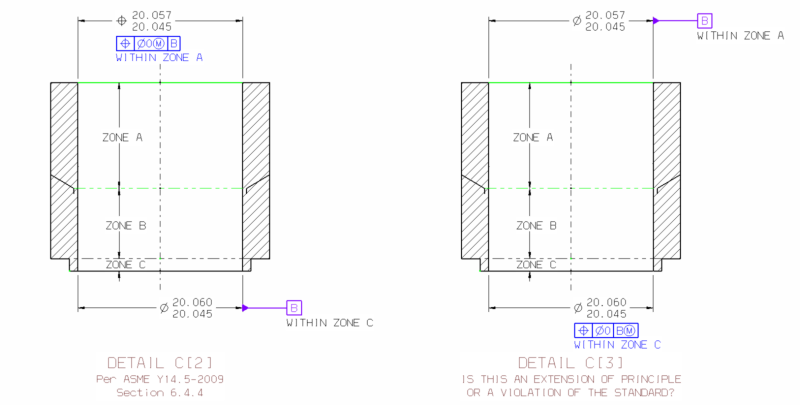
The MMC modifier was specified as MMB in conjunction with switching the Datum and Geometric callouts, to keep the bonus/shift with the same limit dimension.powerhound (Mechanical) said:Unless leaving the MMC modifier was a typo (right hand figure) it's a bad callout.
Besides that, these will not yield the same results. Only on perfect parts will that happen. Don't be surprised to see a significant difference.
I did the two sketches, and did my best to lay out the virtual conditions to try to understand the reasoning behind the request.Belanger (Automotive) said:It violates the standard, but I'm trying to verbalize the reasoning of the question.
In both cases, the reasoning leads me to the same the same layout of the geometry.pylfrm(Mechanical) said:It seems to me that two schemes are exactly equivalent.
I'm coming up with exact equivalency. It is the legitimacy I am trying to ascertain.3DDave (Aerospace) said:The zones aren't exactly equivalent, but both versions are legitimate.
I think you just helped to trigger why I didn't see the fallacy in this earlier. If two features were related back to Datum B at 0 RFS, the simultaneous gaging would ignore the shift produced by an MMB callout between the two features. The two features would be stipulated to be zero tolerance RFS to each other, where 0 at MMC would permit tolerance as the features moved toward their LMC counterparts.Belanger (Automotive) said:Perhaps the issue lies in how such a thing could be measured. Since there's no MMC modifier, you can't use a functional gage. You'd need a gage that is variable or something that outputs a number. So... how can any instrument verify a perfect part? (That's what the zero tolerance RFS means.) To what accuracy?
Assuming a hard gage is not used, for an undoubtedly legitimate |pos|0(M)|B(M)| callout, if the size of Unrelated Actual Mating Envelope (UAME) of toleranced feature equals its MMC size, and the size of UAME of datum feature B equals its MMC/MMB size, the toleranced feature must be perfectly coaxial with datum axis B, right? So does it mean that such actual part condition is impossible to verify?J-P said:Perhaps the issue lies in how such a thing could be measured. Since there's no MMC modifier, you can't use a functional gage. You'd need a gage that is variable or something that outputs a number. So... how can any instrument verify a perfect part? (That's what the zero tolerance RFS means.) To what accuracy?
What if the simultaneous requirement was overriden by use of SEP REQT note?weavedreamer said:If two features were related back to Datum B at 0 RFS, the simultaneous gaging would ignore the shift produced by an MMB callout between the two features. The two features would be stipulated to be zero tolerance RFS to each other, where 0 at MMC would permit tolerance as the features moved toward their LMC counterparts.
If the standard were to adopt |pos|0|B(M)|, any and all simultaneous gauging between two or more of such instances would have to mandate the SEP REQT caveat.pmarc (Mechanical) said:#2. What if the simultaneous requirement was overriden by use of SEP REQT note?
3DDave said:There are a lot of non-functional legitimate combinations that aren't proscribed by the standard. Dealing with them would make the standard very large indeed.
mkcski said:under what real-world design conditions would this dimension schema be used? I think its good for case-study but not much else.
