Yuchi Kang
New member
Hello everyone,
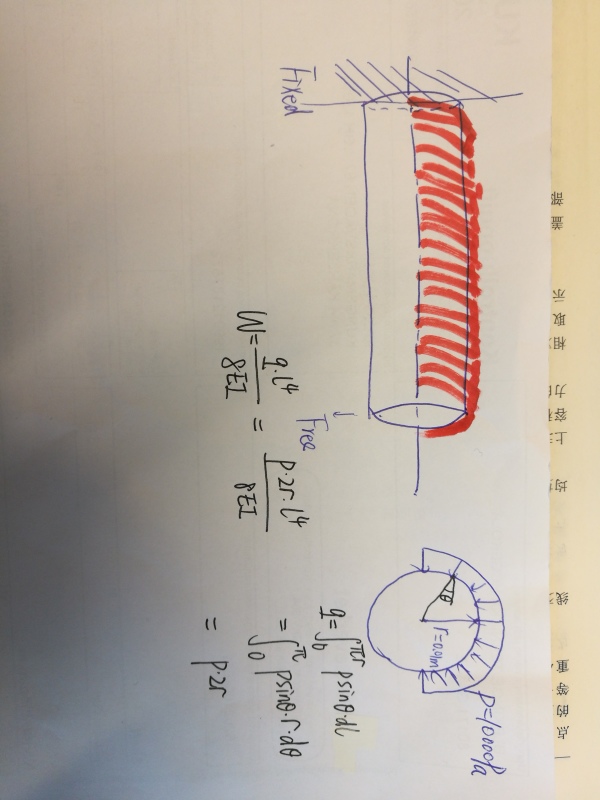
I am trying to calculate the max deflection u2 of a cantilever beam. The cross-section is circle whose radius (r) is 0.01m and length (l)is 1m.One end is fixed and one end is free. This beam is subjected to a pressure on its upper circumferential surface with 10000Pa. In order to verify this model, I calculate the deformation in this way:
p*2r*(l^4)/8/E/I
E is 210*10^9Pa, I=pi*(2r)^4/64
The hand calculation of deformation at the free end is 1.516mm. However, the numerical result is 1.627(for C3D8I) and 1.704 (for C3D8R).
What's the reason for this discrepancy?
Yuchi
I am trying to calculate the max deflection u2 of a cantilever beam. The cross-section is circle whose radius (r) is 0.01m and length (l)is 1m.One end is fixed and one end is free. This beam is subjected to a pressure on its upper circumferential surface with 10000Pa. In order to verify this model, I calculate the deformation in this way:
p*2r*(l^4)/8/E/I
E is 210*10^9Pa, I=pi*(2r)^4/64
The hand calculation of deformation at the free end is 1.516mm. However, the numerical result is 1.627(for C3D8I) and 1.704 (for C3D8R).
What's the reason for this discrepancy?
Yuchi

