A few questions on stress concentrations, yielding, strains, etc. 1

[bugbus]

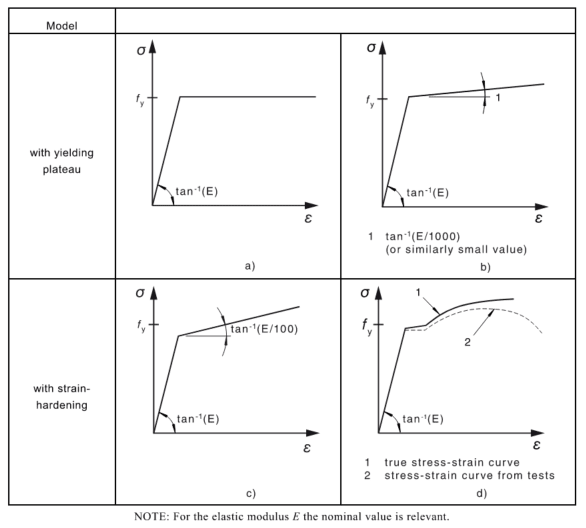
I am trying to learn more about FEA using nonlinear materials to assess the capacity of steel structures, components, brackets, etc.

I understand that when using linear-elastic analysis around sharp notches, re-entrant corners, and the like, there will always be a stress concentration that approaches infinite stress with increasing mesh refinement. I realise also that in a real structure, the geometry never really comes to a perfectly sharp corner if we 'zoom in' far enough, and in any case, the material will locally yield around those stress concentrations and tend to 'even out' the large stress peak predicted by the linear-elastic analysis.

I suppose my first question is this: if we use a nonlinear material in the FEA (e.g., assume an elastic-perfectly plastic stress-strain curve for steel), how do we then interpret the stresses around notches, re-entrant corners, etc., assuming there is yielding in those regions? Are the results sensitive to mesh refinement in the same way that a linear-elastic analysis would be? Or does the use of a nonlinear material tend to be more 'forgiving' in the sense that it smooths over those large stress peaks?

My second question is along the same lines, but more related to strain. Clearly if we're happy to allow the material to yield, we then need to consider the failure criterion being excessive strain by checking that strains are within the capacity of the material. My question is similar: how sensitive are the strain values to the mesh refinement around notches and corners? I suppose I am mainly concerned with situations where tearing may occur in those locations. Note that I'm only concerned with monotonic/static loading, not really about impact, fatigue, etc.

I appreciate any advice in advance, references to books/papers would be really helpful, thanks all

 

[FEA way]

1. Plasticity allows for stress redistribution and much more realistic stress results around notches.
2. Perfect plasticity is not a very good model. It doesn't allow the stress to increase beyond yield and may cause convergence issues. It's better to add some hardening. The analysis will just fail to converge when the plastic strains are too large and full capacity is reached.
3. You should check not only the maximum values of plastic strains (usually the equivalent plastic strain variable called PEEQ is used for this purpose) but also the area subjected to yielding and relate them to codes/standards applicable in your case.
4. Regarding mesh sensitivity, it's always good to carry out mesh convergence studies. Plasticity will just let you avoid stress singularities. If you want to know how much you need to refine the mesh to get good results, you could prepare some simple benchmark similar to your cases (or use your actual models simplified to the minimum) and do such mesh convergence studies for them.
5. There are some interesting articles about this on the Enterfea blog. For example, the ones titled "Materially nonlinear analysis – how does it work", "Flow Chart: Do I need nonlinear material?" and "How to Interpret FEA Results?". Some cover mesh convergence and stress singularities too.

 

[NRP99]

To your both questions, one single answer could be -mesh convergence study. Simple steps-perform mesh with size 1 and note down peak stress/strain/any other result parameter to control and change the sizes to lower size 0 or higher size 2. Do this until 3 consecutive sizes have result parameter varation within 5% or any particular % depending on your application.

Interpretation of results around notch/stress concentration after performing non-linear analysis would be straight forward. The linear elastic/linear elastic perfect plastic material model is not depicting "actual" material behaviour.(I would argue about perfect plastic model for checking redistribution of stresses, anyway). So whatever stress/strains at notches you see for elastic-plastic material model is approx close to reality.

Any plastic strains above yield would need justification (from codes/standards/allowable criteria) of why you would need to allow it. You may establish the failure criteria to be total strain of 5% as per Eurocode or simillar.

 

[bugbus]

FEA way / NRP99, thank you both for your detailed replies. That gives me a lot more to think about going forward.

You both touched on the elastic-perfectly plastic material property potentially not being appropriate for this kind of analysis. Could you elaborate on that a bit further?

The relevant standard I'm working to is AS 5100.6 (Australian standard for bridge design (steel)), which suggests the following:

The elastic-perfectly plastic assumption is sort of implied in a lot of the analysis we already do, e.g., in determining the plastic section capacity of a beam. But I have heard in the past that it can lead to convergence issues (never had a problem personally though).

Again, thanks for the help

 

[rb1957]

I'm surprised that the code doesn't allow Ramberg-Osgood parameterisation. Ramberg-Osgood is a well practiced elasto-plastic material curve, with parameters derived for aerospace materials. If developed for new material would be similar to stress-strain curve from tests (option c might be close) ... the big question is how much testing?

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[NRP99]

You both touched on the elastic-perfectly plastic material property potentially not being appropriate for this kind of analysis. Could you elaborate on that a bit further?

No. This is not implied in my response.We still use elastic perfect plastic model for structural as well as pressurised component. That is why I wrote I would argue about EPP model. Rather structural/energy industry standards recommend to use this model as AS5001.6 suggested.

The EPP model capacities would be conservative and less than EP model but close. Convergence issues are not much of concern as you rightly said.

 

[bugbus]

@NRP99 I see what you meant now, thanks for clarifying