Definitely helps.
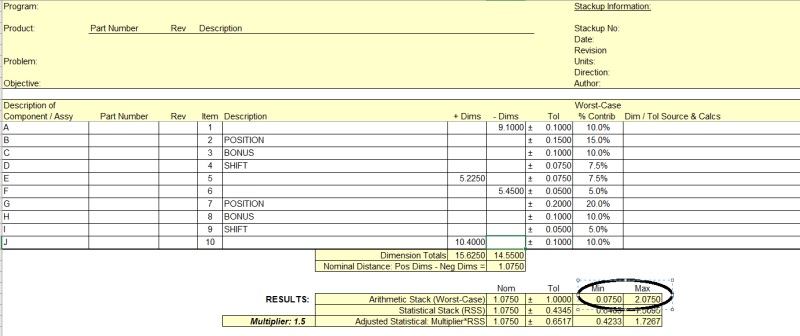
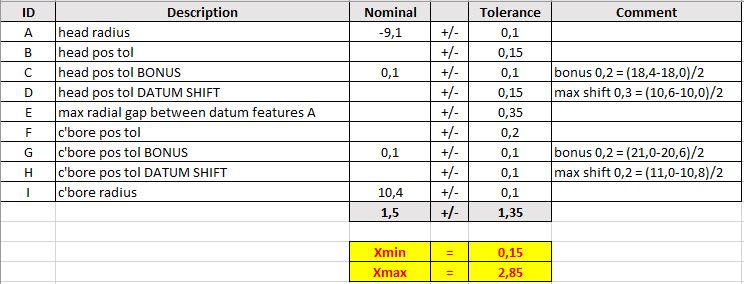
Thank you for your revised stacks. As a matter of fact, I got RSS=1.015 (same as yours for method #2—Single/ Standalone Stack). YEY!! Somehow, I got confused with the calculations for independent (X max and x min, method#1, Two Stacks).
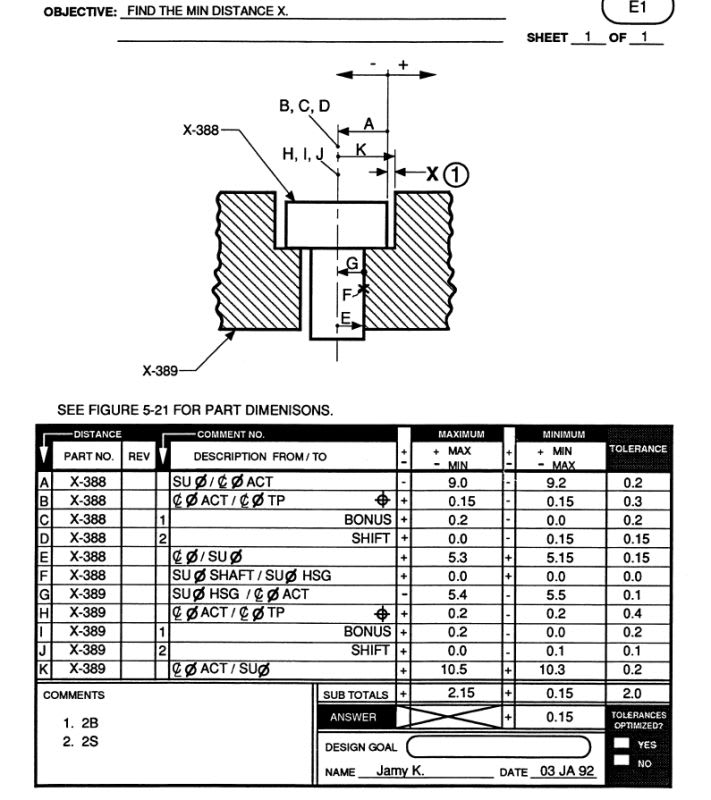
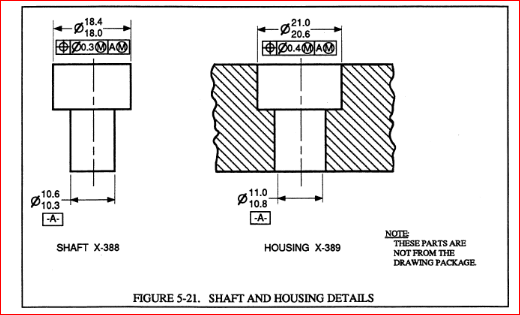
Interesting example regarding the RSS calculations.
Full disclaimer: I do not have access (or knowledge to use) for any variation and/or statistical analysis software like VSA, 3DCS, CeTol, etc. I am curious how the software(s) are handling these kind of RSS calculations (as for W-C calculations the results should be the same). Which method is used by which company? I would say this is extremely simple example, (only two parts involved), so should not be a big issue.
Pmarc,
Do you know if there would be differences between these packages (or any other packages you were expose to)?
I suspect there would be (because why not?).
I just would like to ask you (if it’s not a proprietary/secret information) are you using any of these variation analysis software?
Not sure if I should say, “I wish the company I am working for has one” or those analysis will just create more problems/ issues/ disagreements than solve.