Analysis of concrete trusses

[fa2070]

Hi,

I'm in the early stage of the design of a precast concrete truss... actually a counterfort (see reference [red][sup][3][/sup][/red] for an example). My initial goal was to investigate which arrangement, of all the known truss configurations and their combinations resulted in the fewest tension members for my load case (see [red][sup][1][/sup][/red] for a starting point).
For analysis purposes I couldn't model it as a pure truss, ideal case in which we have axial forces only, no shear, no flexure. One reason is that it's not easy to implement hinges at every node as pure trusses mandate. The other reason is that I assume the same section for concrete chords, struts and diagonal members, so no moment release at the elements' endpoints either.

Having said that, I started the iteration with the truss seen below:

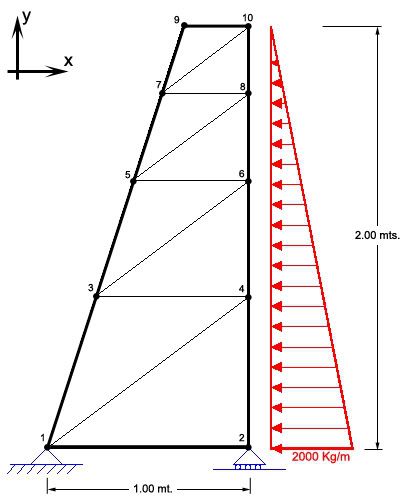
And then I got stuck. The forces (axial, shears, moments) are very very sensitive to variations of E.I [red][sup][2][/sup][/red] and the problem is that I don't yet know what the final "I" will be. I just had to pick a tentative "I" to proceed with the analysis, which might or might not end up being the design E.I.
I found that minor increases or decreases in "I" give completely different results. Even the sign of some axial forces are different!

So my question is: How can I arrive at a truss design with the fewest tension elements when I have such a tight dependency on an unknown (cross section) and not so much on the arrangement of the elements per se?
To add to the mess, if I swap the restraints at nodes 1 and 2 I get a whole different set of results in terms of the magnitude of the forces and signs.

Opinions appreciated.
Thanks.


[red][sup][1][/sup][/red]

http://www.geocities.com/Baja/8205/truss.htm

[red][sup][2][/sup][/red] Which is obvious for statically indeterminate structures.

[red][sup][3][/sup][/red]

 

[Teguci]

If your goal is aesthetics then pick something pretty.
If your goal is cost then use a wall (less complicated reinforcement).
If your goal is to have the fewest tension members then go with a single triangle and support your 2m high wall at the top and bottom. An alternative is to go with a modified King Post with a 3rd compression strut to the midheight of the wall.

 

[miecz]

If the results are sensitive to the support configuration, I would try to model both supports as springs in the horizontal direction, or perhaps even a series of springs along the bottom member.

It's surprising that the results are so sensitive to IE. I would need more information (properties, dimensions) to offer any real suggestions.

 

[Lion06]

I think it is sensitive to changes in relative EI. If the EI for all of the members are the same, then it shouldn't change the results one bit if the EI for all members changes by the same %.

 

[InDepth]

Here are some options:
1) Configure it so it acts like a moment frame without diagonal truss elements
2) Configure it so your diagonals are all in tension and use rods instead of a concrete section (also this ensures pinned connections)....that or use steel sections with a pinned end.
3) Instead of diagonals, just infill the panel so it acts like a shear wall for the bottom two bays. Infill with concrete or masonry (confined masonry system).

One item to note: You should envelope the case of fixed and pinned connections. What you will find is that in a seismic event the connections will start hinging (not fully though), and load distribution will occur and will act more like a pinned truss.

With the situation of I's it sounds like certain members aren't acting effectively.

 

[fa2070]

Thanks everybody for the replies. Highly appreciated.