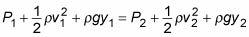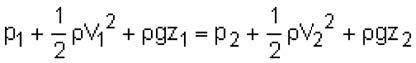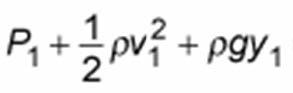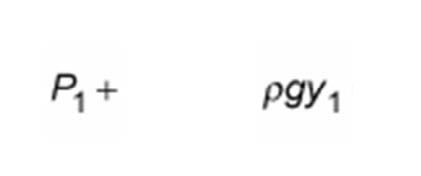solidspaces
Mechanical
- Dec 8, 2011
- 44
According to Pascal’s Law, the pressure inside a chamber that is full and pressurized with a fluid is constant.
Does this imply that the static pressure at the base of the pressurized chamber like a very tall column of pipe (in the vertical position) is the same as the static pressure measured at the top of the pipe?
Should the pressure be measured at the top or the bottom of these pressurized pipes to conduct the leakage test which is usually done at about 14 bar pressure as per NFPA?
Does this imply that the static pressure at the base of the pressurized chamber like a very tall column of pipe (in the vertical position) is the same as the static pressure measured at the top of the pipe?
Should the pressure be measured at the top or the bottom of these pressurized pipes to conduct the leakage test which is usually done at about 14 bar pressure as per NFPA?