AS 3600-2018 Simplifed Shear Capacity for Slabs

[Settingsun]

For one-way (beam) shear of slabs (without stirrups) using the simplified method of clause 8.2.4.3, does item (a) apply? The specific exemption for slabs regarding minimum shear reinforcement has been deleted (8.2.1.7).

If 8.2.4.3(a) applies, the design stress is 0.10*sqrt(f'c) compared with 0.17*sqrt(f'c) previously stated in a few places (eg AS 5100.5-2004, the Warner et al 'Concrete Structures' textbook). Is this reduction real (old structures unconservative) or the standards committee just being more conservative for simple methods?

 

[Toby43]

Steve,

I'm not familiar with the 2018 code yet, but the Canadian code which it appears to be taking much of its provisions from has for their "Simplified" method the following
vc=(beta)sqrt(f'c)
where
beta = 230/(1000+dv) ---------> This assumes longitudinal strain = 0.85X10-3
which would require a 1300mm thick slab to end up with 0.1. Typical slabs would have 0.18 or so.
When my 2018 code arrives in the post I'll have a closer look, but something appears amiss if you are getting 0.1

Toby

 

[Settingsun]

Thanks, Toby.

AS3600 factor 'kv' is the same as your beta. The clauses I'm looking at are below. If there's a slab exemption, it's either somewhere else I haven't seen or you (and your reviewer) are just meant to know that the beam minimum doesn't apply to slabs.

Interesting that AS3600 has a similar equation to Canada (more conservative factors though) but it only applies to sections with <min shear reinf. The capacity is capped quite low which is fair enough for unreinforced beams but out of step with past practice for slabs.

 

[Toby43]

Interesting, as I said I haven't got a copy of the 2018 code yet (I am in Australia), so if a slab exception is present I'm not sure where to look.
That simplified method assumes long strain approx 1.05x10-3.

The Canadian doesn't have any limit related to beta (kv) except that the long. strain need be exceed 3x10-3.
0.1 seems to be an very low value to me, its influence on design I'm yet to have a closer look at. Does the "general method" impose such a limit?
The minimum area of steel has also jumped up 33% - Canadian still has 0.06sqrt(f'c)b/fy. Might start to get tough placing concrete past all those stirrups, which is a very bad idea in my opinion - what good is the concrete strut mechanism if concrete placement becomes increasingly difficult, leaving poorly consolidated concrete in critical high shear zones.

 

[rapt]

steveh49

8.2.1.6 is the clause that controls when minimum is required and it covers beams and slabs. It is currently under review as it is far less conservative than earlier codes for beam shear. It is the same as previous codes for slab shear.

8.2.1.7 should not have the term "beam" in it. This applies to any cross-section.

I will have to look into the numbers for the simplified method and where the .1 came from. Have you compared it with results for the general method?

 

[rapt]

steveh49

Where in AS3600-2009 was there a minimum shear strength of .17*sqrt(f'c) for one way (beam) shear for slabs? There was one for punching shear, and that has not changed in the 2018 code.

 

[Settingsun]

Hi Rapt,
The 0.17 lower limit was in the bridge code until last year (AS 5100.5 clause 9.2.1; D<300mm).

I haven't done much with the 2018 general method yet. Having looked at the method, I'm not a fan for routine (hand) design. I think I've reached that point you often see in American engineers not adopting new codes: "I'm using the Green Book from nineteen-aught-three and haven't had a problem yet". If kv=0.15 can be used for slabs that don't have stirrups, I don't think I'd bother with the general method aside from pushing hard for extra capacity in an existing structure.

However, the general-method minimum value for kv is 0.073 for sections with minimum shear reinforcement, and about the same for slabs without shear reinforcement (some dependence on depth). The strain calculation depends on both M* & V* and I think I need to do some algebra to re-arrange it and plug in some reasonable estimates to get a feel for it.

Equation 8.2.1.6(1) does seem a bit relaxed given how we've been cautioned about the sudden and brittle nature of shear failure in the past. I assumed the 0.10 limit in the simplified method took this into account and that it would be reflected in the general method also, but that doesn't seem to be the case.

EDIT: I've just realised that the 2018 code doesn't allow beams with <min shear reinforcement (I think 8.2.1.7 should refer back to 8.2.1.6 otherwise it strictly applies to all beams regardless of 8.2.1.6) although Rapt says this is an error. So the equations I'm looking at must (only) apply to slabs and walls (until 8.2.1.7 is corrected).

 

[rapt]

steveh49,

Your interpretation of 8.2.1.6 and 8.2.1.7 is incorrect.

8.2.1.6 tells you when you need to provide shear reinforcement (and is under review).

8.2.1.7 tells you the minimum that needs to be provided when shear reinforcement is required. And yes, it has increased by 33% over previous codes. I am trying to find out how it was modified from .06 to .08 after the Draft for Comment was released.

I am also checking on the .1 limit in the simplified method. I would guess that it is limiting the use of the simplified method to lightly loaded sections and requires the more accurate calculations to be done for more heavily loaded sections.

 

[Settingsun]

I've done some algebraic manipulation of the General Method equations to get a feel for what they mean in practice. I've done two cases:

A) Minimum M* as given in 8.2.4.2.2(a)
B) M* = phi.Mu (approx.), called M*max below.

The assumptions include:
[ul]
[li]No prestressing or axial force[/li]
[li]phi(bending) = 0.85; phi(shear) = 0.70[/li]
[li]dv = 0.9*d[/li]
[li]Fy = 500 MPa; Es = 200 000 MPa[/li]
[li]M*max/dv = 0.85*Fy*Ast (ie lever arm of tension-compression couple = dv = 0.9*d; tension force = phi(bending)*Fy*Ast)[/li]
[/ul]
Setting V*=phi.Vuc then means that kv can be found by solving a quadratic equation:
0 = a*kv^2 + b*kv + c

For Case A (minimum bending moment): a = sqrt(f'c)/(84.6*p); b = 2.5; c = -1 (where >Asv,min provided) or -1*1300/(1000+kdg*dv) (<Asv,min; see equation 8.2.4.2(1)).

For case B (~maximum bending moment): a = sqrt(f'c)/(169.3*p); b = 6.485; c = same as Case A.

Where p = reinforcement ratio = Ast/(b*d).

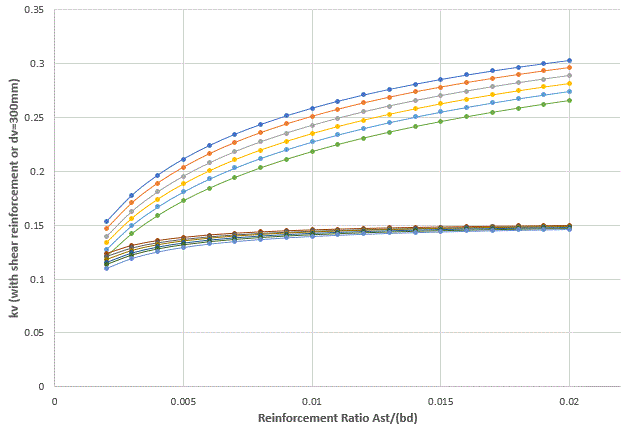
In the graph below; the upper rainbow is for Case A (f'c=20 to 65 MPa from top to bottom); while the lower rainbow is Case B (20 to 65 top to bottom again). This graph is for sections with >Asv,min; otherwise for dv=300mm only. For other depths of sections with <Asv,min (in the range 200<dv<1500mm), this graph is a reasonable approximation to:

Case A: kv/(DF^0.7)
Case B: kv/(DF^0.9)

Where DF = depth factor = 1300/(1000+kdg*dv).

So the Simplified Method factors pretty much assume the section is ~fully utilised in bending. For <Asv,min, a lower bound is used; >Asv,min uses close to (but not quite) the lower bound.

Next task is to plot AS3600-2009 to see how it compares given it had no dependence on bending moment.

PS I know what the standard is trying to say in 8.2.1.6 & 8.2.1.7 regarding when beams don't require shear reinforcement, but some words that appeared in previous versions of the code have been omitted and it no longer says precisely what it used to say IMO.

 

[rapt]

PS I know what the standard is trying to say in 8.2.1.6 & 8.2.1.7 regarding when beams don't require shear reinforcement, but some words that appeared in previous versions of the code have been omitted and it no longer says precisely what it used to say IMO.

That is not what you said in the previous post!

 

[Settingsun]

Hi Rapt,
It's what I was trying to imply (when I said 'strictly' and 'until corrected'). It's academic for me since I won't design a new beam without shear reinforcement anyway. I have seen a few times where a reviewer will 'dig in' on a literal interpretation of a code so sometimes it pays to read carefully as a devil's advocate if your work is going for external review. I recall one case where I was a spectator and the very-experienced design engineer justified his design by explaining who wrote the particular section of the code, what the intention was, and why it didn't apply in this case. The even-more-experienced reviewer essentially replied "Noted, however the design criterion is compliance with AS5100." The design had to be revised.