The thread744-499791 is closed. To continue discussing, I created this new thread.
In a former posting by Doug (IDS(Civil/Environmental)in the thread, he stated:
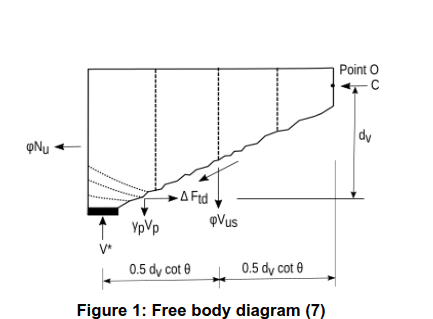
"Case 3 is just using the AS5100.5 code formula for the longitudinal force due to shear, and finding the adjusted bending capacity, allowing for the force. Increasing the shear reinforcement reduces the longitudinal force, so increases the bending capacity."
as a response to my query:
"Could you please describe the steps in your calculation for Case 3 which resulted in an increase in bending capacity from an increase in the area of shear reinforcement ?"
My understanding of the analysis described in Doug's blog (link provided in thread744-499791) is as below.
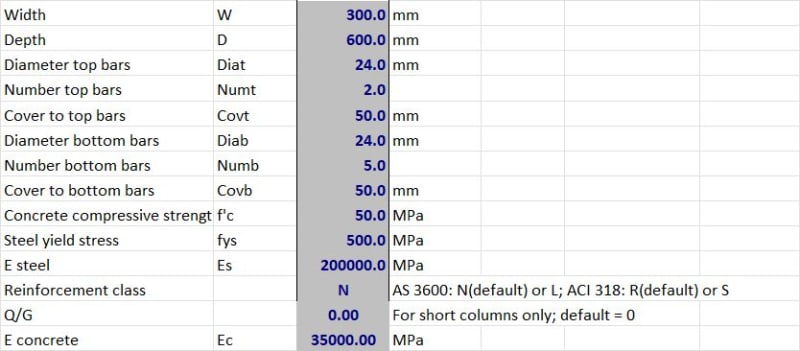
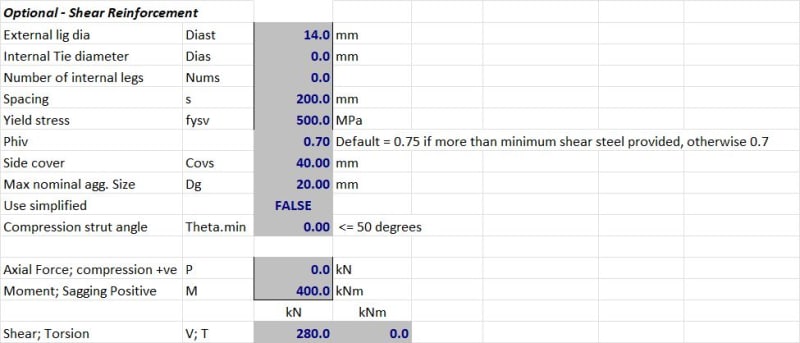
The total longitudinal steel Ast1 is first determined for shear reinforcement Asv1/s for a section with design shear V*1, ultimate shear strength Vu1 such that the axial force in Ast1 is close to fsy under combined action effects M*1 and V*1. The shear reinforcement is the increased to A_sv2/s with the following values kept the same:
Vu2 = Vu1,
V*2 = V*1
Ast2 = Ast1
A new moment effect M*2 is then determined through trial and error (or iteration) so that Ast2 is close to fsy.
Owing to M*2 determined being greater than M*1, it was concluded that an increase in the shear reinforcement caused an increase in "reduced moment capacity"
Doug,
Before I discuss further, I would like to check whether my description of the analysis above is accurate.
In a former posting by Doug (IDS(Civil/Environmental)in the thread, he stated:
"Case 3 is just using the AS5100.5 code formula for the longitudinal force due to shear, and finding the adjusted bending capacity, allowing for the force. Increasing the shear reinforcement reduces the longitudinal force, so increases the bending capacity."
as a response to my query:
"Could you please describe the steps in your calculation for Case 3 which resulted in an increase in bending capacity from an increase in the area of shear reinforcement ?"
My understanding of the analysis described in Doug's blog (link provided in thread744-499791) is as below.
The total longitudinal steel Ast1 is first determined for shear reinforcement Asv1/s for a section with design shear V*1, ultimate shear strength Vu1 such that the axial force in Ast1 is close to fsy under combined action effects M*1 and V*1. The shear reinforcement is the increased to A_sv2/s with the following values kept the same:
Vu2 = Vu1,
V*2 = V*1
Ast2 = Ast1
A new moment effect M*2 is then determined through trial and error (or iteration) so that Ast2 is close to fsy.
Owing to M*2 determined being greater than M*1, it was concluded that an increase in the shear reinforcement caused an increase in "reduced moment capacity"
Doug,
Before I discuss further, I would like to check whether my description of the analysis above is accurate.