ASCE 7 Two Stage Seismic Analysis 4

[cdowney4]

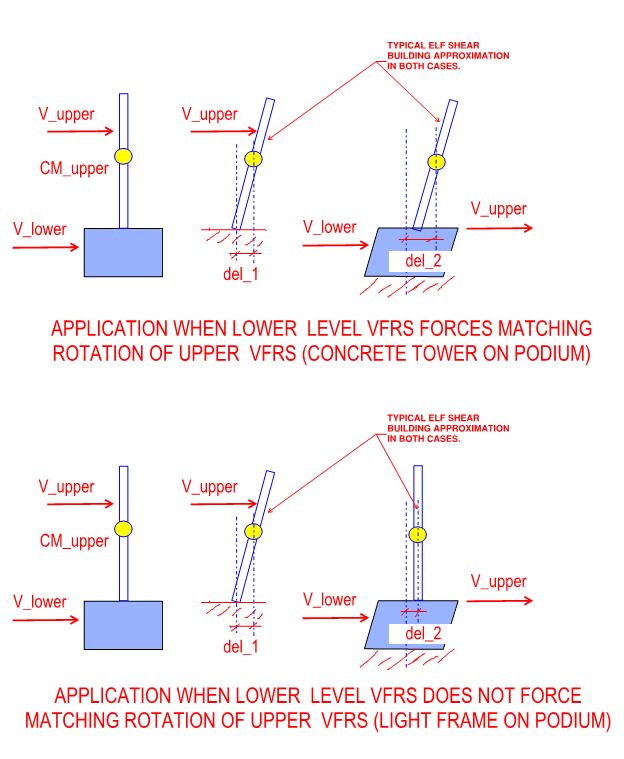
When looking at the ASCE 7 Two Stage Analysis Procedure, there seems to be an anomaly that bothers me and I'm wondering others opinions/experience. In terms of seismic forces, it seems to me that the two stage procedure can be quite beneficial for the upper level light-framing, but can be penalizing on the lower rigid structure (and foundations).

What bothers me is that I could look at it per 12.2.3.1 (ASCE 7-10) for Vertical Combinations and potentially get an overall lower base shear/overturning on the building, but a higher distribution of forces on the upper levels. Or, I could look at it per 12.2.3.2 as a two-stage and get lower distribution of forces on the upper, but larger overall base shear and overturning for the building.

What I would really want to do is design the lower portion per 12.2.3.1 and the upper per 12.2.3.2. It seems pretty clear that is not the intent of the language of the code, but the practical side of me says that if I took the penalty on the upper framing by just using 12.2.3.1, I have a code-complaint lower portion of the structure with lower design forces. But if I design the upper per 12.2.3.2, all of a sudden that same dsign for the lower portion is not code compliant? How does the lower portion know what design methodology I used or what forces the upper levels were designed for?

In my particular current case, I'm looking at a building that is 4 stories of wood framing over 3 stories of P.T. slabs and concrete shear walls, so perhaps this anomaly is more severe than a single level rigid lower portion.

Am I way off on this type of practical thinking? Even if I am not, perhaps I am just yelling at the clouds.

 

[driftLimiter]

Unfortunately I can't dig into this discussion in detail right now. But here is a link to a structure magazine which addresses similar concerns with the dual stage procedure. In my experience the penalty on the upper levels (wood floors carrying some proportion of concrete floor seismic mass) is hard to deal with, which seems to be the original intent of dual stage procedure.

[URL unfurl="true"]https://www.structuremag.org/?p=19539[/url]

 

[KootK]

Am I way off on this type of practical thinking?

I believe so. As with load path & stiffness in general, it's somewhat less important that your assumptions are correct and more important that they are consistent throughout your analysis. I don't like the idea of telling one story about the building's dynamic response for the upper levels and a different story for the design of the lower levels.

 

[ggcdn]

I guess there is a third option, which is to do a dynamic analysis of the entire structure. I think that would land somewhere between the two-stage and the ELF-single structure approaches.

I've heard some people are doing this for wood frames, but oh boy does it not look very fun.



-JA
try [link calcs.app]Calcs.app[/url] and let me know what you think

 

[KootK]

I've heard some people are doing this for wood frames, but oh boy does it not look very fun.

As in light frame wood buildings? I'd be hard pressed to see the value in that given the wild uncertainty in the stiffness of wood panel shear walls.

 

[driftLimiter]

@cdowney4 The article that I posted covered some specific concerns with dual stage that I think are a bit different from what you are saying. I am curious whether the presumption that dual stage overly penalizes the podium level is actually correct. A case-study would surely help, but it's gonna take some effort lol.

Both methods require scaling of the forces from the above structure to the below structure, and in a combined analysis, the seismic mass of the podium is all still represented, however some of it would be 'pushed up' into the building. I fail to see how the base shear would be less, and in my mind we should expect more overturning would be more if seismic mass of podium is distributed to higher levels. I guess we would just need to see some numbers on it. Sure the diaphragm load at the podium levels would be less using a combined analysis, but the MLFRS should see the same base shear at perhaps more overturning.

Although as @Sonofatkins and @KootK have pointed out, the dynamic analysis of lightframe wood construction is problematic. I think that using code required deflections as the basis for stiffness, one could use the a dynamic model to test the assumption of the dual stage analysis. Supposedly if you make the podium rigid enough it will become uncoupled from the upper structure, this could be tested with a dynamic study. I wouldn't go using the dynamic results for strength design but it could shed some light on the dual stage assumption.

Anyone have time to make a case-study for us? haha perhaps next time I'm traveling I could work up come models.

 

[KootK]

I am curious whether the presumption that dual stage overly penalizes the podium level is actually correct. A case-study would surely help, but it's gonna take some effort lol.

I was wondering the same, particularly once all of the penalties arising from mass and stiffness irregularities are properly applied to both methods. I've no reason do doubt OP's experience but the results are a bit of a surprise to me.

 

[cdowney4]

Thank you all for the thoughts so far. I will re-visit my initial whack at the forces and see if I am correct, and then share some numbers. The project isn't ready for a full analysis yet, so I was just trying to gather my initial thoughts on my approach, and haven't even modeled anything yet. I will admit that I've only done a few podium projects in my career, so my ELFP spreadsheet that I've been using for years isn't quite equipped to automate the two-stage approach (although maybe it should and will be soon...)

By ELFP, when looking at the lower 3 stiff levels by themselves as part of the two-stage procedure, I was seeing a significant decrease in the estimated period as compared to looking at it as one building (with the lower 3 stiff levels plus the 4 upper flexible stories). It was about T(est)= Cu*Ta = 0.46 vs. 0.85. Hopefully I didn't make some simple error in my haste, but will come back here with my tail between my legs if I did.

 

[ggcdn]

@driftLimiter - have fun! [URL unfurl="true"]https://wood-works.ca/wp-content/uploads/Linear-Dynamic-Analysis-for-wood-based-shear-walls-and-podium-structures.pdf[/url]

-JA
try [link calcs.app]Calcs.app[/url] and let me know what you think

 

[ggcdn]

I am curious whether the presumption that dual stage overly penalizes the podium level is actually correct

but the results are a bit of a surprise to me

In my mind the penalty is from the base shear calculation using different period between the lower and upper structures. To exaggerate the situation, and get rid of the difference in R values for a second, consider a high-rise consisting of 36 story concrete tower sitting on a 4 story concrete podium.

Case 1: you have 1 overall period, Tcombined, and a total weight, Wcombined for a 40 story building. Base shear will be V = Cs(Tcombined)*Wcombined.

Case 2: you have podium and tower periods, Tp and Tt, and corresponding weights Wp + Wt = Wcombined. Base shear will be V = Cs(Tp)*Wp + Cs(Tt)*Wt.

For a tall building, the difference between Cs(Tp) and Cs(Tt) will be immense, because the podium will have a period of <0.5sec while the tower could be up at 5sec. One will be at the peak of the response spectrum, one will be in the long-period valley. The difference between Cs(combined) and Cs(Tt) will be negligible. They will likely be governed by the cutoff minimum value.

So a two stage approach has effectively stripped off some mass excited at a low Cs, and applied a high Cs to it. This is the 'penalty', I think.

-JA
try [link calcs.app]Calcs.app[/url] and let me know what you think

 

[driftLimiter]

At the root of our discussion here is the fact that we are performing a simplified dynamic analysis. The overall structure, when combined analysis is used, has a big stiffness and mass discontinuity. It seems that the dynamic response of this type of structure is going to be different than a structure with a more uniform distribution of mass and shear. Perhaps some other mode shape carries more mass participation for the overall structure and it is this period that should be used to determine the base shear. ASCE7-16 C12.8.2 alludes to this oft unused principle regarding the period determination....

...The fundamental mode of a structure with a geometrically
complex arrangement of seismic force-resisting systems determined
with a three-dimensional model may be associated with
the torsional mode of response of the system, with mass participating
in both horizontal directions (orthogonal) concurrently.
The analyst must be attentive to this mass participation and
recognize that the period used to compute the design base shear
should be associated to the mode with the largest mass participation
in the direction being considered. Often in this situation,
these periods are close to each other....

I am so curious now how a detailed dynamic model would compare with both methods.

These issues remind me of a paper by Ed Wilson. Interestingly it used to be up publicly on his website and now the link is broken. It is a rather contentious article for an engineer if I do say so myself.
Here is the paper Link

 

[sticksandtriangles]

What a fun read driftlimiter, thank you for the link.

I am all on board for the removal of response spectrum analysis! Too many odd quirks to it and the analysis often yields close to meaningless values taken at face value.

S&T -

http://www.re-tug.com

 

[KootK]

My overall impression of this is that, for the right kind of building:

1) The simplified, two stage, ELF analysis method should be sufficiently accurate and;

2) The "punishing" loads that the two stage method produces on the podium level are the right loads. This makes perfect sense to me for the "right" kind of building because:

a) If it's flexible over very rigid, as intended, then there's little doubt about the upper stories delivering load to the lower as if the lower were a fixed base.

b) If it's flexible over very rigid, as intended, then the standard shear building approximation that throws faux mass from the podium up to the upper structure is invalid. The substantial mass inertia of the podium structure belongs with the podium structure.

The trick is in determining what kind of buildings are the "right" ones. And, frankly, I feel that we could do this much better than ASCE currently does it. See my proposal below where the metric of interest would be something like del_2 / del_1 < 0.1 (or whatever limit makes sense). In particular, note how this would play out differently for two very different kind of buildings:

a) Buildings where the podium LFRS enforces a matching rotation of the upper LFRS would be far less likely to qualify for two stage. Less concrete towers.

b) Buildings where the podium LFRS does not enforce a matching rotation of the upper LFRS would be more likely to qualify for two stage. More light frame over tanks.

 

[cdowney4]

OK, I am back with some numbers to share, and it seems to be what I thought.

For my building, when doing the Two-Stage procedure, I’m finding the total base shear and total base overturning to be about 78% and 36% higher, respectively, compared to looking at the entire structure as one building with the lower R value.

BUT, when looking at is as one building, the base shear and overturning for the wood framing increase by about 77% and 62% respectively.

For those looking to play along at home and check my numbers, here’s what I have.
- 7 structured levels
- Level 4 (third structured level) is the podium. Levels below are concrete shear walls (R = 5). Levels above are wood (R = 6.5).
- ASCE 7-10, Ss = 0.352, S1 = 0.106, TL = 6, Ct = 0.20, x = 0.75
- Soil Site Class C
- Snow pf = 33.6 psf


Level Mass (k) Height Above Grade (ft)
2 (concrete) 4347 k 9.00
3 (concrete) 4347 k 21.00
4 (concrete) 5541 k 33.00
--------------------------------------------------------------------------------------
5 (wood) 1108 k 43.67
6 (wood) 1108 k 54.33
7 (wood) 1108 k 65.00
8 (wood) 1294 k (w/ 20% snow) 76.67


These are my results:

BASE OF BUILDING:
Analysis Approach Vb (k) – TOTAL @ BASE Mb (k-ft) – TOTAL @ BASE
One Building (R = 5) 530 24,107
Two-Stage (R = 6.5 & 5) 945 (78% increase) 32,878 (36% increase)

BASE OF WOOD FRAMING:
Analysis Approach Vw (k) – @ WOOD base Mw (k-ft) - @ WOOD base
One Building (R = 5) 271 (77% increase) 8,154 (62% Increase)
Two-Stage (R = 6.5) 153 5,032


I will hold my thoughts for a moment and let the numbers speak for themselves. If anyone sees any errors or flaws, let me know.

 

[cdowney4]

Sorry for the bad format on the tables. I wrote my message elsewhere and then cut and pasted it here. The tabs/indents didn't come thru properly...

 

[Mike Mike]

"Do not be called a Neanderthal man"! lol thanks story drift limit!

Koot K., I agree with the first half of your post, not sure I follow the second half. What is del? It seems to me rotation plays a bigger role on buildings with small footprints and shorter shear wall lengths. Is it your intent to make it harder for tall slender buildings to qualify for 2-stage?

Mr. Downey, not sure I follow your numbers toward the bottom there man, probably because of the tab issue. Could you confirm the reason you get a higher base shear using the 2-stage procedure is lower periods, meaning higher Cs values (as suggested by story drift limit's Structure Mag link, paragraph 4)?

 

[Mike Mike]

One more thing before I hit the hay here, hoping you guys can help me out. I'm doing a 4-story light frame wood gyp shear wall over 2-story concrete moment frame building, you guys know of an easy way to justify that the period of my entire structure isn't greater than 1.1 times the period of my wood portion [ASCE 7-16 12.2.3.2 (2)]? Koot K. I'm looking your way

Based on the period equations of ASCE I definitely don't qualify. Accounting for actual stiffnesses per the FEMA 450 Eq. C5.2-1 Rayleigh method might get me there, but my coworker says this method assumes roughly even stiffnesses all floors. Not sure I agree with him.

Per story drift limit's structure mag link above "although compliance with [the 1.1 rule] is not uniformly adhered to, the provision at least helps diligent practitioners and code enforcement officials keep designs closer to the code intent of a fixed base." By this I assume he means that a lot of engineers just don't check it.

I'm trying to avoid using software or getting lost in the weeds here. I'd like to do a quick, approximate calc to show I qualify for 2-stage.

 

[driftLimiter]

Remember the provision doesn't say to compare the periods but the stiffness. Perhaps if you back-calculate the stiffness from the code estimated periods, this could be an easy way to get the values K upper and K lower.

Other than that, a better way to do it might be :
1) Assume you meet the requirement and carryout the 2 stage analysis.
2) Calculate the stiffness for the upper floors by a rigidity analysis of the shearwalls following NDS or IBC equations.
3) Calculate stiffness of the lower lever. ACI provisions for concrete deflection.
4) Compare at the and iterate as required. Not clear whether you would use the inelastic displacements including deflection amplification for this calculation. Perhaps thats most conservative.

The concrete moment frame building might tend to be pretty flexible, I've only used concrete shearwalls in the podium. I think the structure mag article isn't a good reason to avoid adherence to the rule.

 

[Mike Mike]

Drift limit, doesn't [ASCE 7-16 12.2.3.2 (2)] say "The period of the entire structure shall not be greater than 1.1 times the period of the upper portion considered as a separate structure fixed at the base."? Why do you say I don't need to compare periods?

 

[driftLimiter]

Ahh yes period is the 1.1 and stiffness is 10x sorry I didn't think of which part you were looking at. I was thinking of the stiffness comparison check alone.

You could use the stiffness of the lateral system and the mass to estimate the period as well perhaps a better approximation than the basic equations in the building code.