RM12
Mechanical
- Jan 29, 2024
- 32
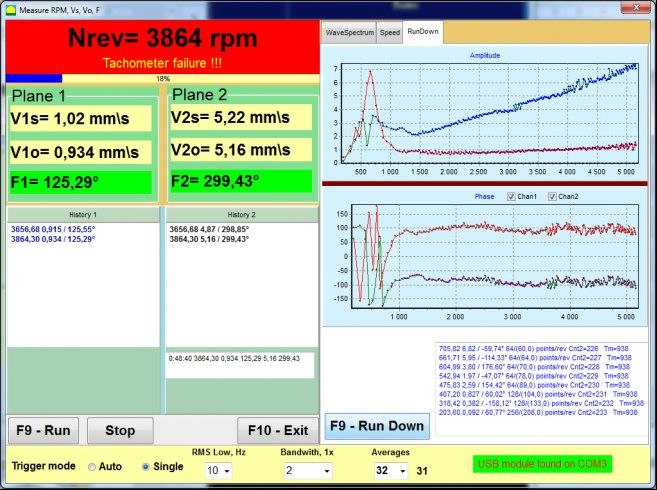
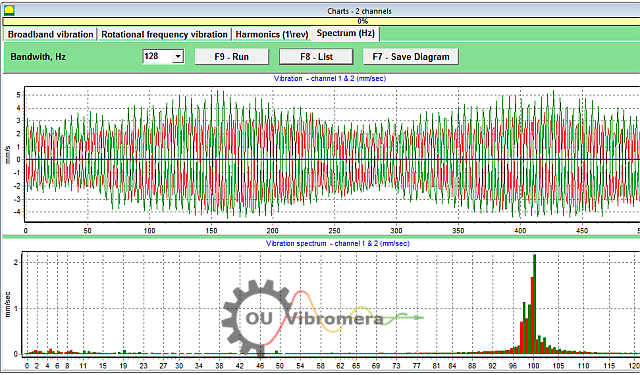
I have been working on trim balancing a motor (Vertical pump motor) that was reconditioned. I was wondering if anyone has approached balancing vertical motors placed on a rubber pads (1/2 inch thick) to simulate a pump head attached in the field. Of course, the motor is clamped down on an isolation bed but with rubber pads between it. It is not clamped too tight which otherwise would be the same as placing it on the isolating bed without it.
Are there any existing papers or experiments done by others on this?
Thank you
Are there any existing papers or experiments done by others on this?
Thank you