Beam buckling help.

[asv4k8]

So i have a 'c' channel beam as shown here: The beam i used is marked with red

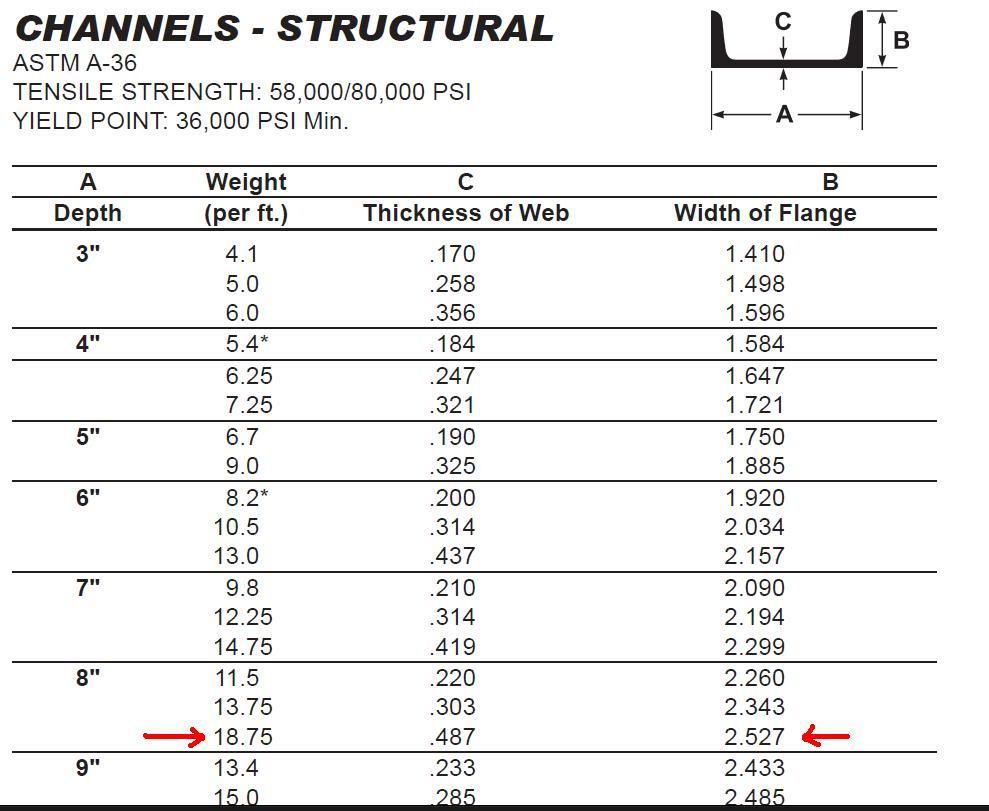
I assumed the whole beam to be of thickness C (.487") in this case.. found my moment of inertia to be Ixx=1.80621in^4

Here is my eulers formula

Fcr = (pi^2 x E x I)/L^2 I used english standard units which i think are correct but see if i am correct here:

E for astm a36= 200gpa = 29007547.54psi
I is my moment of inertia in inches^4 = 1.80621 (using the 8" beam with thickness of .487" and spars of 2.527")

Fcr = (3.14^2 x 2907547.54psi x 1.80621in^4 )/216"^2 = 11072.126 lbs before one beam buckles..

does this sound right or did i loose something in the units/math error?




As always thanks in advance and if you need ANY automotive engineering or performance advice feel free to email me as I am not on here that often.

 

[boo1]

AISC gives Iyy=1.98, assume your L = 216 in

dont forget to add in KL is the effective length of the column

K = column effective length factor, whose value depends on the conditions of end support of the column, as follows.
For both ends pinned (hinged, free to rotate), K = 1.0.
For both ends fixed, K = 0.50.
For one end fixed and the other end pinned, K = 0.699....
For one end fixed and the other end free to move laterally, K = 2.0.

 

[asv4k8]

do you have the formula with KL added?

As always thanks in advance and if you need ANY automotive engineering or performance advice feel free to email me as I am not on here that often.

 

[hokie66]

You called it a beam, but are apparently using the channel as a column. Is this correct? Channel shapes are very inefficient when used for compression members.

 

[JAE]

I assumed the whole beam to be of thickness C (.487") in this case..

I hope you know that the thickness of the web is different than the thickness of the flanges.

 

[Lion06]

The 11 kips you came up with is a nominal critical buckling load. This needs to be reduced by a factor of safety to compare to an actual load.

This is a grossly inefficient column, though. I don't have a steel manual in front of me, but using 490pci for steel with 18.75 plf, I come up with an area of 5.5 sq in. That equates to a radius of gyration of 0.6. This means your kl/r is 216/.06 = 360. This is incredibly high.

Not to mention, the nominal buckling stress is 11kips/5.5 sq in = 2 ksi. 2000 psi is an incredibly low buckling stress and indicates an inefficient use of material.

 

[irizarry]

Limit States Per AISC (360-05 Specs Section F):

If you're using the angle for flexure (as a beam):

-channel bent about major axis (rotated 90 degrees from your picture):

1. Yielding: Mn=Mp=Fy*Zx
2. Lateral Torsional Buckling:
a) L<Lp, the limit state doesn't apply
b) Lp<L<Lr, Mn=Cb(Mp-0.7Fy*Sx((L-Lp)/(Lr-Lp)))<Mp
c) L>Lr, Mn=Fcr*Sx<Mp

where:
Fcr=Cb*pi^2*E/(L/rts)^2(1+0.078J*c/(Sx*ho)(L/rts)^2)^0.5
Lp=1.76ry*sqrt(E/Fy)
Lr=1.95rts*E/(0.7Fy)*(J*c/(Sx*ho))^0.5(1+(1+6.76(0.7Fy*Sx*ho/(E*J*c))^2)^0.5)^0.5
rts^2=(Iy*Cw)^0.5/Sx
c=ho/2(Iy/Cw)^0.5 -> for channels
Cw= Warping Constant
ho=dist. between flange centroids

-channel bent about minor axis (same as picture):

1. Yielding: Mn=Mp=Fy*Zx<1.6Fy*Sy
2. Flange Local Buckling:
a)Compact flanges (lambda=bf/(2tf)<lambda_p):
FLB doesn't apply
b)Non-Compact flanges (lambda_p<lambda<lambda_r):
Mn=(Mp-(Mp-0.7Fy*Sy(lambda-lambda_p)/(lambda_r-lambda_p)
c)Slender flanges (lambda>lambda_r):
Mn=Fcr*Sy

where Frc=0.69*E/lambda^2
lambda_p and r come from table B4.1 of the AISC 360-05 Specifications:

lambda_p (flanges)=0.38(E/Fy)^0.5
lambda_r (flanges)=1.0(E/Fy)^0.5

If you're using in unifrom compression (as a column), just say and I'll write the equations.