DavAD
Structural
- Nov 20, 2017
- 8
Dear all,
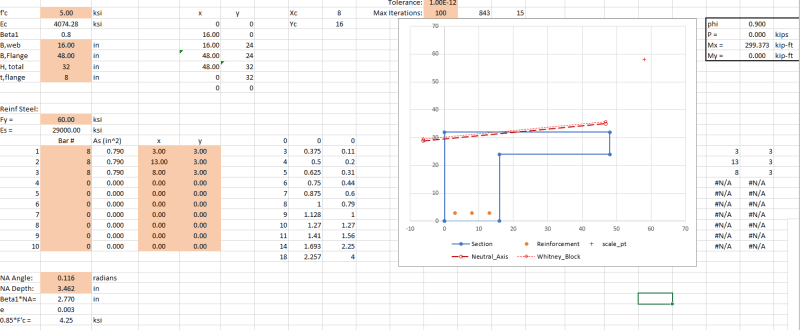
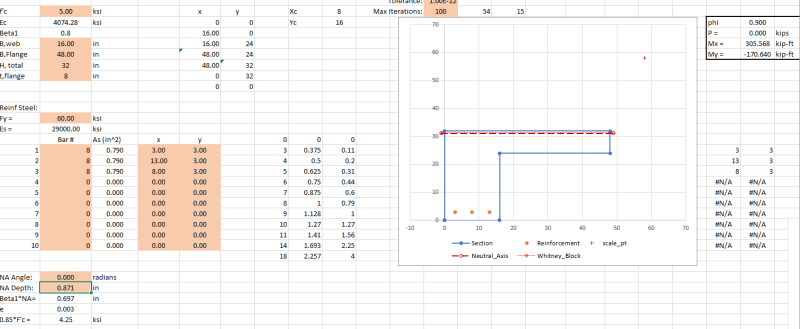
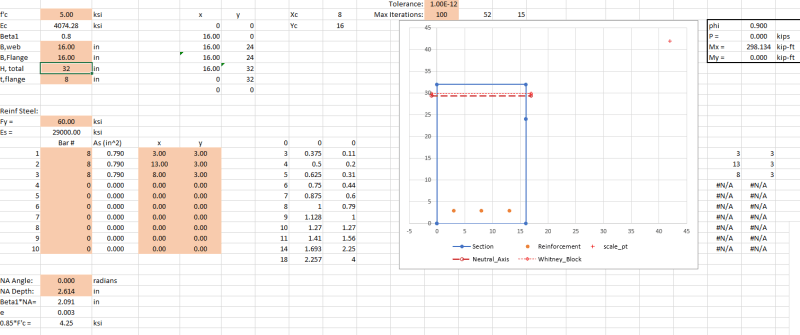
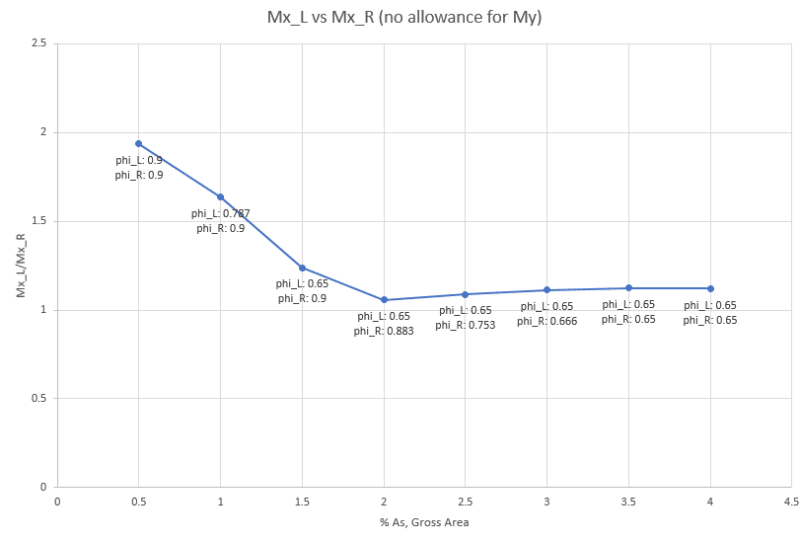
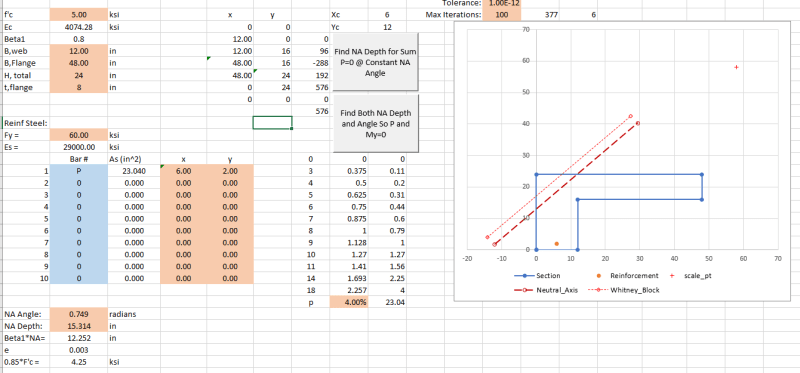
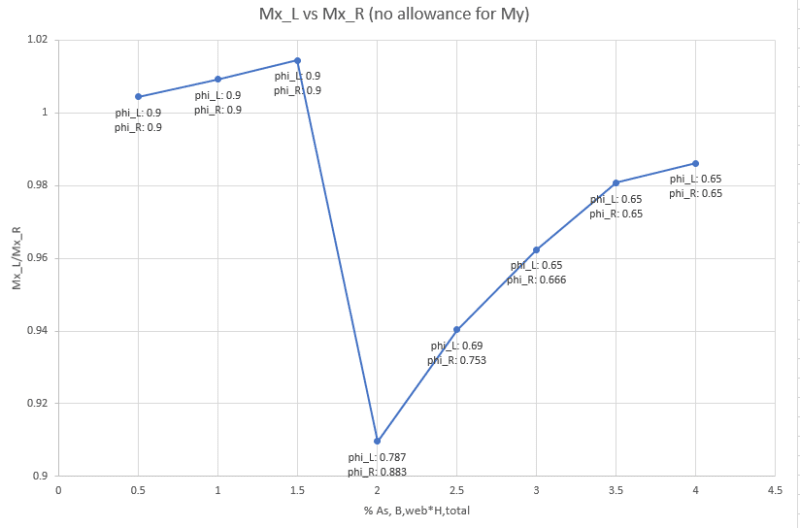
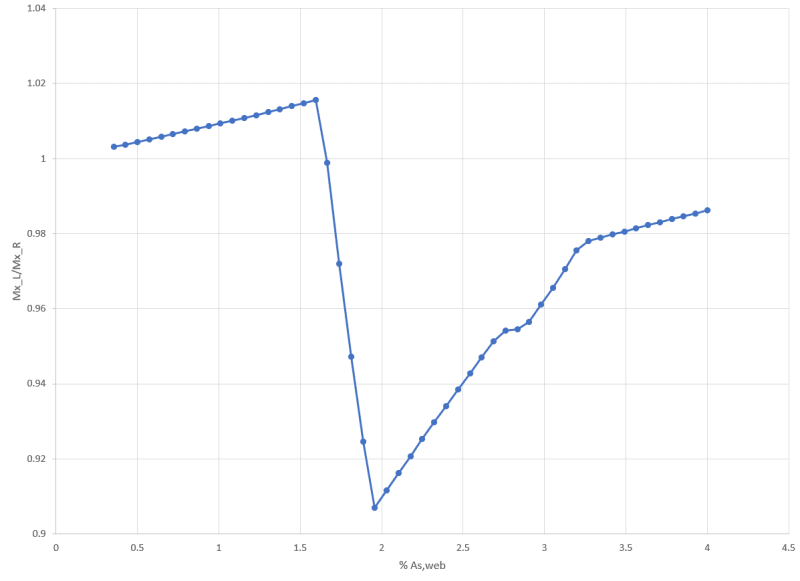
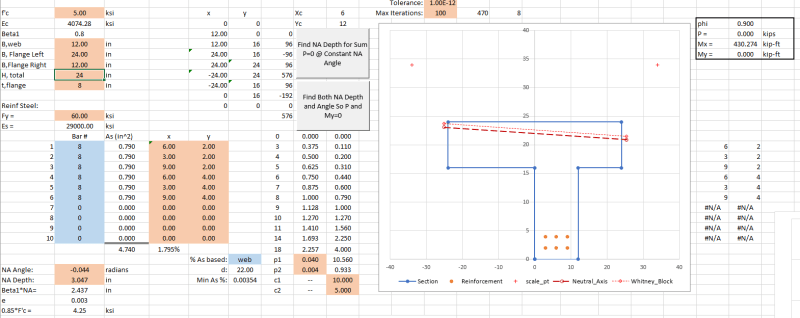
I have attached two scenarios of a reinforced concrete beam carrying a horizontal slab.
In principle, would you say that in Scenario B, the beam has a higher load capacity than in Scenario A, considering that the whole depth is beneath the actual slab load, whereas in the other case (A) the load is 'hanging' at the bottom of the beam.
P.S. The beam has in both cases been designed for the slab load, supported by the beam.
Your comments are greatly appreciated.
Kind Regards
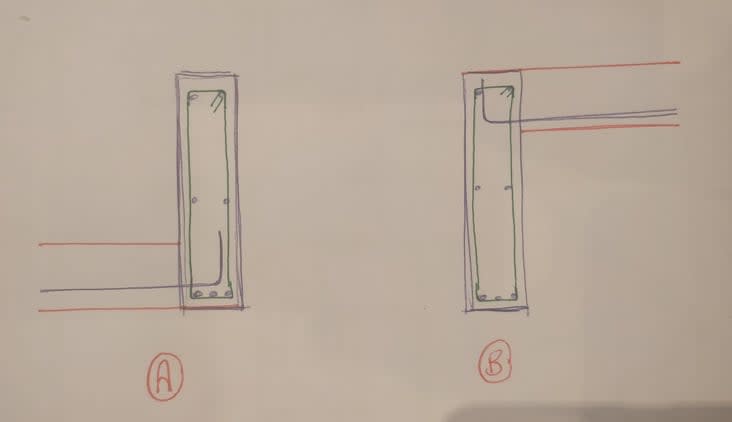
I have attached two scenarios of a reinforced concrete beam carrying a horizontal slab.
In principle, would you say that in Scenario B, the beam has a higher load capacity than in Scenario A, considering that the whole depth is beneath the actual slab load, whereas in the other case (A) the load is 'hanging' at the bottom of the beam.
P.S. The beam has in both cases been designed for the slab load, supported by the beam.
Your comments are greatly appreciated.
Kind Regards