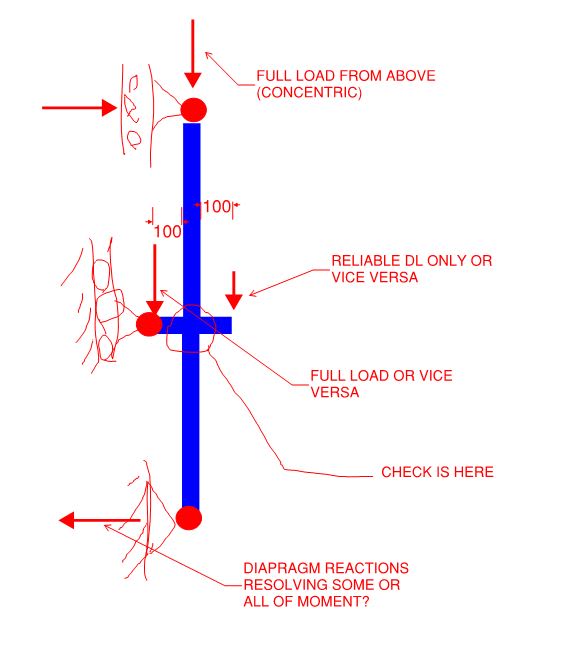
human909 said:
Damn you does that mean that since I agreed with you earlier I need to flip flop too?
We'll see how it goes. I'd be grateful if you'd help me vet it.
THE THEORY
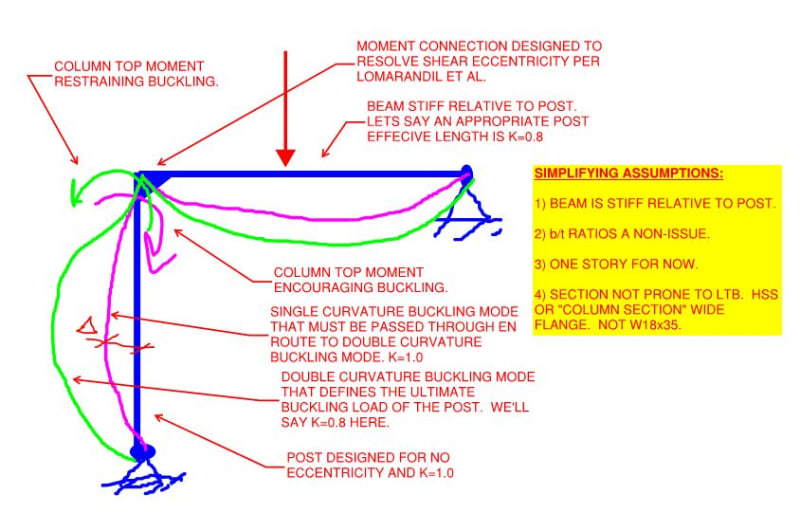
1) Model per the sketch below.
2) Make a bunch of simplifying assumptions that I feel are pretty reasonable for a gravity post.
3) I contend that the process of column buckling may be envisioned as occurring in two phases:
a) Magenta; single curvature; [K = 1.0]; column top moment encourages buckling; design case; load eccentricity to RIGHT of post centerline.
b) Green; double curvature; [0.7 < K < 1.0]; column top moment restrains buckling; ultimate buckling capacity; load eccentricity to LEFT of post centerline.
At the limit of the single curvature mode shape, the apparent flexural stiffness of the post drops to zero
for the single curvature buckling mode. This causes it to kick to the left until it engages the stiffness of the beam as rotational restraint.
4) In transitioning from magenta to green, the post must pass through a moment in time where [e = 0; K=1; design case]. Moreover, after the post passes through this moment in time, it's capacity continues to increase. So this moment in time represents a lower bound on in-plane buckling capacity.
5) I see one hiccup with #4. At the moment in time described, the column is not yet shifted to the left enough to reach equilibrium. Another way to look at it is that it's an [e = 0; K = 1.0] design with a baked in displacement, delta, that adds to the normally assumed column imperfections. So the "moment in time" column capacity is some degree lower than that calculated at [e = 0; K = 1.0]. I feel that the impact of this is going to be small will relatively stiff beams and larger with relatively flexible beams since, the larger the beam stiffness, the less movement is required to re-establish equilibrium.
SOME TAKEAWAYS
I feel that this theory supports some of the limitations that many engineers are already applying as a matter of intuition and judgment. Namely, if one is going to ignore the eccentricities in a gravity post in favor of a nominal moment connection:
1) It should be a stocky, post appropriate section like an HSS, W14, etc. It should not be a W12x14, W18x35, or anything else with relatively narrow flanges and an affinity for LTB.
2) The [EI/L] of the beam(s) should be relatively stiff compared to that of the post. No limp noodles, no joist seats unless the BC ties in too.