Bending Square section in reinforced concrete 1

[Lhi]

Hello
Im trying to calculate stresses in SLS for a bending square section in reinforced concrete.
It involves to find the neutral axis which is possible with static moment equation.
Here is the distribution of stresses for a square section in diagonal plan from a book:

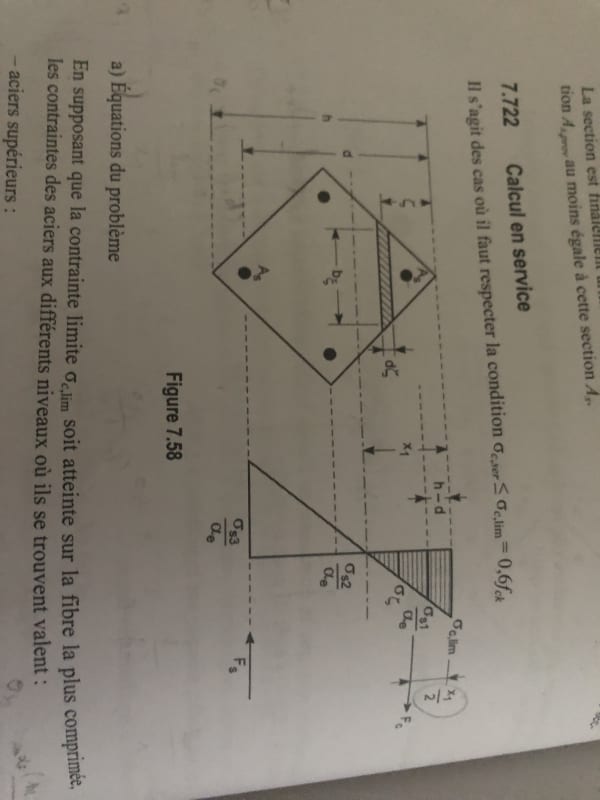
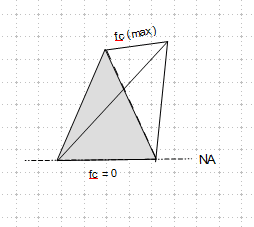
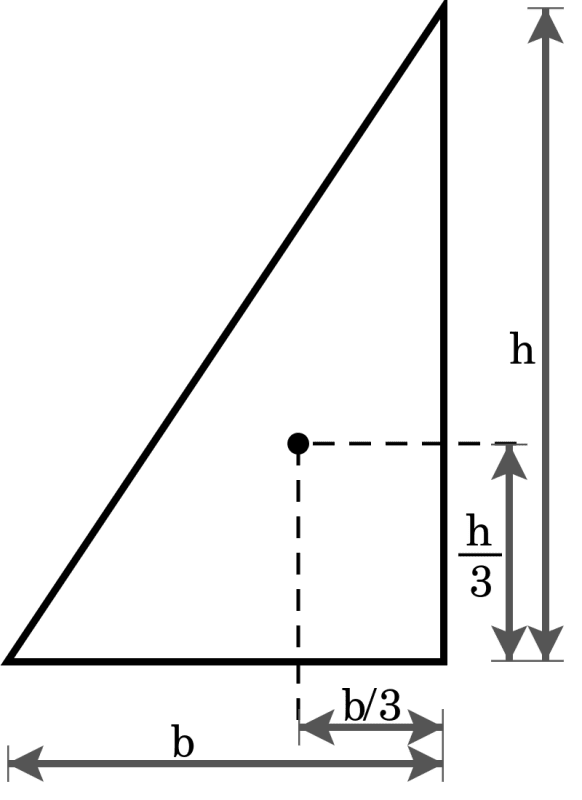
First, I don't understand why the effort Fc is located at x1/2 from neutral axis. The distribution of stress is triangular so why the effort is not located at (2/3)*x1 from neutral axis?

Then here is the equation of static moment from the book :

I don't find the same result because if we say that Fc is at x1/2 we should have x1^3/6 and not x1^3/3, right?

Thank you for your help.

 

[r13]

I think it is the centroid of the volume bounded by the triangle area (fc varies linearly from maximum on the top, to zero at NA).

 

[Celt83]

as Retired indicated you have a linear increasing stress on a linear reducing cross section the result compressive force ends up a the height of the stress block, x1, / 2 in this case.

If your interested I posted the general formulas for a linear varying stress and a piecewise linear section boundary in this thread, second to last post:

https://www.eng-tips.com/viewthread.cfm?qid=460377

My Personal Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

Open Source Structural GitHub Group:

https://github.com/open-struct-engineer

 

[r13]

You can verify the centroid location of this solid volume using auto-cad, or maybe 3D shape builder program.

 

[Lhi]

Thank you both,

@Celt83 I'm trying to understand your formula from the link, thank you.

If I am not mistaken, the centroid of a triangular shape is:

This is why I don't understand that Fc is located at x1/2 from NA..I'm a little bit confused

 

[Celt83]

for a triangular shape that would be the centroid, but in this case you are really looking at a 3D prism. If the stress was constant over the area then you could use the standard 2D triangle centroid but your stress is linear so you need to do the double integral of the stress function to get the volume which is equal to the force, Fc, and another double integral with x or y*stress function which yields the first moments of area which are equal to the My, Mx moments caused by Fc.

My Personal Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

Open Source Structural GitHub Group:

https://github.com/open-struct-engineer

 

[Celt83]

user Agent666 also has a decent blog post on the subject:

https://engineervsheep.com/2020/parabola-10/

My Personal Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

Open Source Structural GitHub Group:

https://github.com/open-struct-engineer

 

[WARose]

I don't know if you have '246 Solved Structural Engineering Problems' (by Buckner).....but they have a problem where they figure a crude, lower-bound interaction diagram for a non-rectangular column (with bending capacity obviously being part of it). It might help here. I used it on a weird shape once myself.

If you have PCA column, it might could generate that info as well. (Although probably with more points.)

 

[IDS]

For any triangular shape with zero stress at the base and maximum stress at the crown, and linear distribution:

With x measured from the base, depth D and base width B:
For simplicity take max stress = D:
Stress = x
Width = B(1-x/D)
Force = Integral(0 to D): Bx(1-x/D) = B(D^2/2 - D^3/3D) = BD^2/6
Moment = Integral(0 to D): Bx^2(1-x/D) = B(D^3/3 - D^4/4D) = BD^3/12

Height of centre of force = (BD^3/12)/(BD^2/6) = D/2

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/