robyengIT
Mechanical
- Dec 20, 2013
- 894
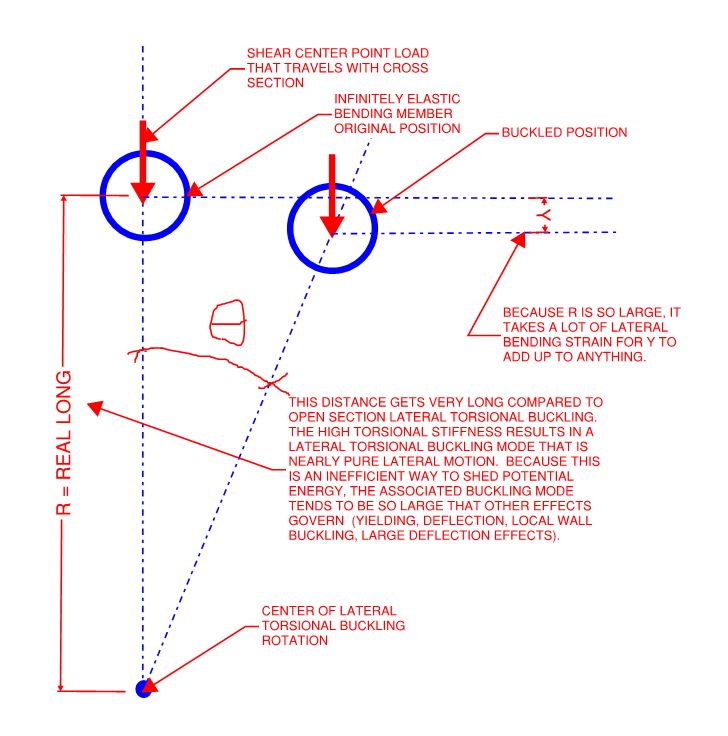
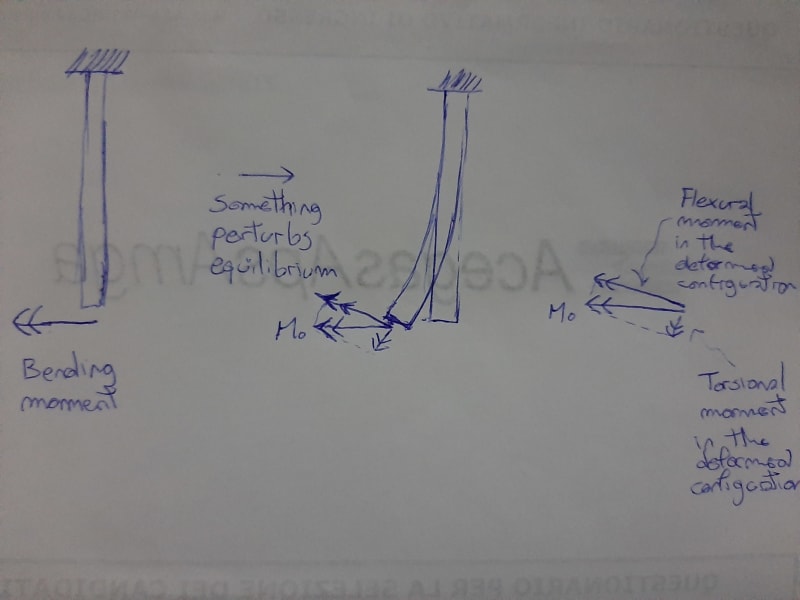
Eurocode says that a steel pipe item (part of a structure) is not affected by a bending+torsion instability (i.e. when the torsion stiffness is bigger than the bending stiffness ??). I am looking of literature discussing and explaining such a statement. Thanks