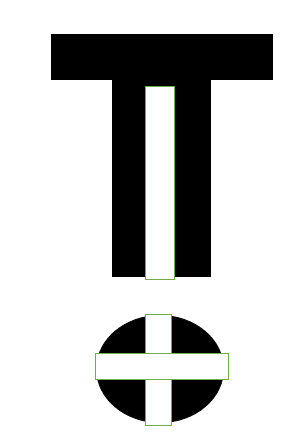BOLT CLAMP FORCE / THREAD STRETCH 3

[Matt206]

Background:
A simple relatively accurate formula to relate Torque to Clamp Force is: T = (F)(D)(K).
Where D --= Diameter of bolt, T = Torque, Lets ignore K for this.
I am encountering a situation where a screw designed like #1 has an appropriate clamp force with the hand toque that we are able to generate. While a screw designed like #2 does not achieve the appropriate clamp force.
Thread type, thread engagement, material, is all exactly the same. As the above formula suggests, the diameter difference is the reason for the difference in holding force. I can actually feel the stretch that I am looking for when turning the smaller screw.

Question:My question is WHY does Diameter have an impact on this? I would think it would be cross sectional-area of the screw, But after drilling a through-hole in the larger diameter screw to decrease the cross sectional area (with the intention of making it function as a thinner spring to generate more stretch) this did not impact the clamp force.
If unable to change thread type, engagement, and diameter – I am unable to achieve the required clamping force with a given torque.

Picture 1:

Picture 2:

 

[rb1957]

1) "Lets ignore K for this." ... let's not, it is important.

2) "accurate" is a stretch ... more like "one size fits all (and none very well)"

3) applied torque is reacted by friction on the thread, that's why "D" is a term (and it fits too, as much as anything fits ...).

another day in paradise, or is paradise one day closer ?

 

[MintJulep]

You have discovered why you cannot ignore K.

 

[dhengr]

Matt206:
And, you have discovered why torque to turn the head of the bolt is not a very good indicator of the holding force/tension on/in the bolt. Diameter, is of course, proportional to the length of the thread bearing or frictional area. But, the friction value is dependent on so many variables which are tough to control that it is tough to put a number on it, and thus, on ‘k’. If you read a little deeper on the subject, you will find that your formula is a very simplistic first approx. or first shot at the problem. It can be made to work under lab. conditions, and in very finely controlled industrial situations, after much research and testing to set values of ‘k’, application procedures, fit and conditions of threads, etc.

 

[chez311]

"Why does diameter have an impact on this?"

For a few reasons. rb1957 hit it on the head with his #(3), additionally taking into account the spring analogy a larger diameter bolt essentially is a stiffer spring. It is not the amount of stretch alone which creates your axial preload - it is the combination of the amount of stretch and bolt stiffness. Think of two springs, of differing stiffness - the one with the lower stiffness will have to stretch more to achieve the same axial force as the one with higher stiffness. This is why drilling a hole in the bolt* did not increase your preload achieved (I assume you torqued each to the same value) - in fact, had you measured rotation you would have found that the one you drilled a hole through had rotated farther (through a larger angle) as it had to stretch more to achieve the same preload. For this reason also (due to the aforementioned issues with variable friction factors) it is far more accurate to measure torque-angle instead of torque alone, as the angle to turn a fastener is a much more reliable measure of preload generated.

*Edit: I should have added that of course that drilling a hole in the bolt reduced its stiffness.

2nd Edit: I also glossed over your first issue with the different sized diameter bolt not achieving the required clamp load as the same torque. As mentioned by others, thats down to the different friction factors of the two bolts.

 

[EngineerTex]

WHY does Diameter have an impact on this?

You are looking at the system incorrectly.

Regarding the engaged thread length: The region of the engaged threads will take on an approximate stiffness of the summation of the fastener and the hole that it is threaded into. For a steel bolt going into a tapped hole in a steel body of some component, the approximate stiffness of the part that is threaded will be around 5x as stiff as the fastener, so the threaded area including the fastener and the steel body is about six times the stiffness of the grip. If you drill a hole through the fastener in this region, you still have an extremely stiff region.

Regarding the grip length: This is the part where the stiffness is simply that of the cross-sectional area. If you drill a hole through the larger fastener to yield the same cross-sectional area as the smaller fastener, then yes, the stiffness of the grip length will be the same.

Recognize that whatever you do to change the grip area has zero effect on the thread engagement region. If you significantly reduce the cross-sectional area of the fastener in the thread engagement area, it doesn't really change much about what is going on in the thread engagement area. As is mentioned above by multiple posters regarding this equation, it is a simplification of what is going on and in this simplification, the controlling factors are the diameter (and thus, the contact area) and the friction.

So why are we talking about stiffness and cross-sectional area? In this equation and in actual fact, the stiffness of this region is irrelevant to this situation. Hypothetically, with zero friction, if you apply torque to a fastener, there will obviously be some force generated, no? But this equation shows that if you applied infinite torque with zero friction, you would develop zero axial force (EDIT) any torque with zero friction, you would have infinite force in the member. (/EDIT) Sounds a little fishy to me. It seems that this equation is simply an approximation that claims that virtually all of your torque simply goes into overcoming friction. Sounds kinda like what you have determined in practice.

To expand a little further about what's going on, you have to recognize that the equation models the screw as being a long wedge wrapped around an axle and that it assumes a very shallow wedge angle. For shallow angles, a.k.a. thread pitch, this approximation is pretty good, regardless of the angle/pitch... as long as it's a pretty shallow angle. Note that this means that according to this equation, a fine thread and a coarse thread with the same active diameter will end up coming up with the same values and you know that these would not be the same. Once again -- this is why you want to use the turn-of-the-nut method, as opposed to measuring torque.

Engineering is not the science behind building. It is the science behind not building.

 

[kiwitom235]

to break it down into most simple form, the friction force applied in the direction of rotation (and hence axial direction aswell using the coefficient of friction relation) at the threads is larger for a smaller diameter when applying the same tightening torque.

Simple gearing... Torque = Force x Distance where 'distance' is radius of bolt, 'Force' would be friction force, and torque is torque.

 

[Tmoose]

What are threads ( nominal diameter and pitch) of bolt 1 and 2 ?

How much torque are you applying to bolt 1?

How much torque are you applying to bolt 2?

 

[drawoh]

Matt206,

What are you turning to clamp the bolt? It looks to me like your first bolt has a larger, easier to turn head.

--
JHG

 

[Matt206]

Hey Guys thanks for all the replies,

Follow up question,

As I have seen in my situation, D has a large impact on the clamping force.
AND From the replies I understand that it is due to the frictional force of the threads, due to the increased circumferential contact area (correct me if I am not understanding that correctly).

So the question is, Do you believe that cutting a few notches in the screw (in order to decrease the frictional force) would allow the bolt to function as if it had a smaller diam?

My instinct tells me No because while there is more thread stretch, there is less holding force per distance stretched due to decrease in thread contact area ---- But this same logic could be applied to the smaller diam. screw -- so i am not understanding something

Something like this:

 

[hydtools]

Maybe change your method to " turn of the nut" rather than torque.

Ted

 

[chez311]

Matt206,

If I understand your figure correctly, you're proposing cutting the threaded/shank portion of a bolt into four sections almost all the way to the head. I would absolutely NOT recommend modifying a fastener in the manner, I could imagine such a design could only find use in the most specialized of applications and would fail spectacularly in almost every other situation - not to mention I highly doubt it would function as you're expecting. Those four sections would collapse on each other as soon as you started applying torque/preload to the bolt. Strength and clamp load would be severely reduced, if you could even get it to achieve anything resembling a reliable clamp load. To take that a step further I would not recommend modifying an off the shelf fastener unless absolutely necessary, and then only after doing the proper calculations and testing to ensure that any modifications (ie: say cutting a groove in the shank of a bolt which would reduce the tensile strength of the bolt significantly) still meet the design requirements.

I apologize if those admonitions are applied to a question that was purely theoretical (ie: what happens if we reduce the contact area of the threads), or just a thought experiment, but I think such a question should not ignore the realities of what is being asked.

Now lets get to the meat of what is being asked:

would allow the bolt to function as if it had a smaller diam

What exactly is the performance that you are finding in the bolt of smaller diameter that you cannot get out of the larger diameter bolt? The same clamp load out of the same applied torque? What is stopping you from just.....(hopefully it's not too simple of me to suggest)....applying more torque to the larger fastener and/or some combination of torque/angle control? If you desire lower torque levels for whatever reason, a thread lubricant (there are many options out there - ARP Ultra Torque is one many engine builders swear by) of can always be utilized to reduce the torque needed to achieve the same clamp load. Note I believe there are some rule of thumb recommendations for the reduction in applied torque, but this should always be verified with testing.

 

[Matt206]

Guys,

These are theoretical examples

This is for a specific Biotech application,,,,, below are not in the realm:
Applying more torque
modifying female threads (thus no change in male thread diam)
Lubricant cannot be used
material cannot be changed

This is handling a very small amount of torque, I was just looking here to see if there was something i was "missing" in concept.

EDIT: in my above quick example, I understand it would collapse, in reality i was imagining a screw that was designed in such a way that it would not have a full thread engagement around the circumference--- but not designed in such a way as to not collapse in 00 im not talking about modifying a off the shelf screw, this would go through testing and be manufactured from scratch,

I just want to know in theory if something like that holds water

But what i understand from above posts, the female threads account for most of the thread stretch.

 

[hydtools]

Turn down the OD for some distance from the underside of the head to just above a minimum length of thread. The necked down shank will stretch like the smaller diameter screw.

Ted

 

[Matt206]

Ted that would contradict what all the other comments above are saying about the Diameters influence due to thread engagement

 

[chez311]

Matt206,

There have been several mentions of "friction area" or "contact area" - as far as I understand friction is independent of surface area (in theory anyway - in practice the waters get a little murky, however that is typically due to other factors/variables). Your only inputs are the friction coefficient and normal force. The additional factor which needs to be considered with a fastener is the diameter - which is essentially a moment arm through which the friction force is reacted. Larger diameter = larger moment arm = larger amount of torque to overcome the same amount of friction. You can see this in the simplified equation you presented T = FDK. If you rearrange and solve for preload (normal force) you get F = T/(DK) and you can see that if torque is kept constant, as the diameter of the fastener is increased the amount of preload generated decreases.

But what i understand from above posts, the female threads account for most of the thread stretch.

Clamp load is generated because the bolt stretches and creates a tensile force. The female threads are reacting the load applied by the bolt - any deformation there would actually be compression and reduce the bolt preload.

I know you said that these questions are theoretical, but since you have mentioned a specific application, and since I presume the end goal is to find a solution for aforementioned application, allow me to ask a few questions:

1) I am curious, what is preventing the application of more torque - especially since as you say it is a low torque application?

2) Is a dry film lubricant or coating in the realm of possibility? Something like this:

https://www.whitfordww.com/wp-conte...ngs-Solve-Friction-and-Corrosion-Problems.pdf

or heck, even something like a geomet/dacromet zinc flake coating will reduce your coefficient of friction.

3) Can you provide more information on the application at hand, as others have asked about? Ie: fastener diameter/length, engagement length, clamp load desired and torque applied (or apparent limits), bolt and female mating thread/component material?

 

[Matt206]

chez,

Wow, I understand the diam/friction relationship now --- I dont know why that wasnt clicking for me with the other comments..

Without going into much detail -- a Hand powered screwdriver is used, cannot change the screwdriver, but tested a T-handle screwdriver and was able to achieve the clamp needed. I have tried lubricating with WD-40 and was not able to achieve the clamp load required, so im pessimistic about the friction coefficient being reduced enough due to lubricant.

I know this isnt enough information to offer solutions, but its probably all im at liberty to mention. I appreciate the comments

 

[hydtools]

Necking down the screw reduces the spring rate resulting in more stretch for a given load.

Ted

 

[Matt206]

Ted, That thinking is in-line my initial thoughts, as you can see in my comments related to Cross Sectional Area --- but The effect is negligible as pointed out in comments above and with what I have witnessed in practice.

 

[hydtools]

Try it. You tried with the hole.

Ted