Bolt pressure through two flanges. 1

[klliq]

I have a question, now let's say I have a pressure vessel that is cylindrical and has two caps on both ends. To make it simple, we only need one nut and bolt for each side. So let's say the force is 1000lbs. So I will find one nut and bolt that will handle 1000lbs on one end of the cap and one nut and bolt that can handle the other end of the cap. Simple. But now let's say if I had a long threaded bolt that will go through both cap, so now I only need one nut and bolt that will go through both caps. Is my force still 1000lbs or is it 2000lbs because there's 1000lbs of force on each side of both caps? So I need to find a bolt that will handle 2000lbs of force? How can the pressure stay the same, yet the force doubled? Or is the force distributed so it's only 1000lbs still?

 

[DriveMeNuts]

I assume that this is a stud with nuts on each end, holding the pressurised caps together.
Perhaps Newtons 3rd law will be of help to solve your thought experiment.

If two bodies exert forces on each other, these forces have the same magnitude but opposite directions.

 

[klliq]

That's where I'm confused. Now if it is only on one side, the surface area of the flange cap is 1000lbs of force, so I can easily size the bolt and nut that is rated for 1000lbs. But if there was two end caps, one on each end, so assuming the pressure is the same, so it's exerting 1000lbs of force on each end of the cap. Then I have a long bolt threaded through both caps. Do I need a bolt that can handle 2000lbs?

Now that I'm thinking about it more, the bolt is now covering the area of both caps, so if each of those caps are exerting an area of 1000lbs of force, then basically the area just doubled, so it has to be 2000lbs.

Just not too obvious, as we were trying to reduce the bolts by replacing the 4 bolts on each side (8 total) with a similar grade bolt but long enough for both caps. So need a higher grade bolt if were were to use one that can close both caps.

 

[GBTorpenhow]

Draw a free body diagram of just the cap for the case with bolts. Pressure x internal area is resisted by the total bolt tension. Now do the same for the case with studs. It's the same diagram. Whether the bolt tension ends up being applied to the back face of the mating flanges (in the case of 2 sets of machine bolts) or straight through to the nut on the other cap (long studs), the bolt tension is the same for both arrangements.

 

[goutam_freelance]

GBTorpenhow is correct!

I elaborate the concept below:

If this is your concept,

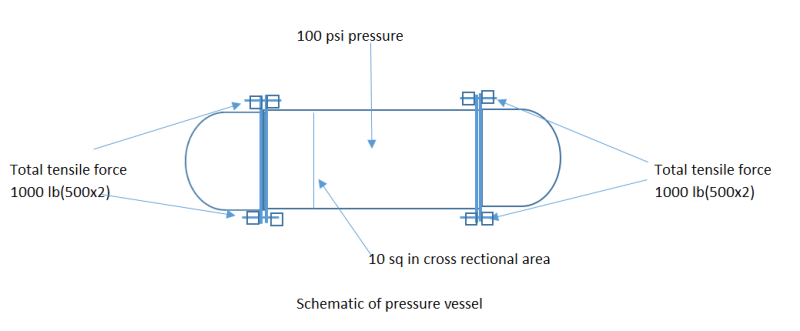
Then the tensile force across through bolt remains same (1000 lbs)as below

 

[Snickster]

You have to look at how the force is transferred. If you have a cap with a bolt on one side and on the other a cap with a weld on the other side then on each side there is a 1000 pound force pushing in opposite directions that balance each other so that as some said by Newtons laws there is no net force so no net acceleration of the vessel. This is because the force of 1000 pounds is transfered through the bolt to the crossectional area of the vessel on one side which is balanced by the force of 1000 pounds on the other cap which is transfered through the weld then into the vessel crossectional area so that it balances the 1000 pounds force on the other side so that net acceleration of vessel equals zero. In other words the force on one side is balance by the force on the other side and shows up in the tensile stress of the vessel wall of 1000 pounds divided by the crossectional area fo the vessel. If you had a bolt through the entire vessel on both heads then no force is transferred through the vessel wall crossection but is transferred only through the crossectional area of the bolts. In either case you have 1000 pounds acting in one direction and 1000 pounds acting in the exact opposite direction so you end up with 1000 pounds of tensile force in the bolt but no tensile stress in the wall of the vessel. Newtons 1st, 2nd and 3rd laws say basically same thing but different ways, that if the sum of forces = 0 then there is no acceleration. Or if there is no acceleration of a body with forces acting on it then the sum of those forces must be equal to zero - the forces are balanced. This is an extremely important point that if a body is at rest but has forces and moments acting on it then those forces and moments must be in equillibrium. This is the basis of all structural analysis.

 

[Trestala]

In actual application, you have to consider gasket relaxation, flange relaxation, bolt relaxation, flange yielding, proper bolt pitch, etc. and not as simple as the responses above. More information has to be provided such as design pressure/temperature, gasket used, and material.

 

[DriveMeNuts]

In one direction you have a force of +1000lb. The other direction you have a force of -1000lb.
When I sum all the forces, +1000lb and -1000lb, I get zero 0lb, not 2000lb.
Perhaps you should check your maths.

 

[klliq]

I would thought the force exerted on each side of the flange is 1000lbs, so if both side is pushing 1000lbs, the total has to be 2000lbs of force exerted. So I need to size a bolt that can handle more stress, ie. a higher grade bolt. I understand the stress on the flange wouldn't change, nor anything else about the system.

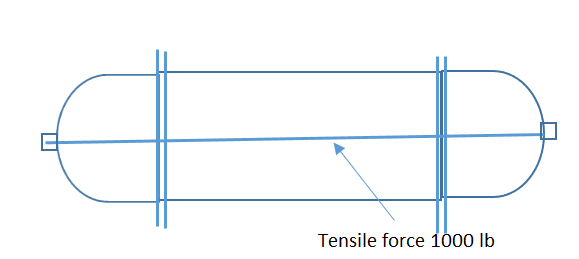
Here's what I meant by through bolts. I simplified the idea just by using one bolt, so I revised your drawing slightly to go with your diagrams, here's what I meant.

 

[GBTorpenhow]

Lets play tug of war. I pull 100 lbs on one end of a rope and you pull 100 lbs on the other end of the rope. What's the tension in the rope?

 

[klliq]

Exactly, I just got confused because the question raised was that if the pressure was the same, why would it double? But then it has to double because the bolt is now handling double the area exerted.

 

[SwinnyGG]

You interpreted the tug-of-war analogy the wrong way.

The tension on the rope is 100 lb.

The tension on your theoretical bolt is 1000 lb. The pressure does not 'double'.

 

[klliq]

The pressure remains constant, but doesn't the force double? So in the case of the diagram of using the through bolts, each bolts is now 1000lbs (total of 2000lbs for both). Or are you saying that the bolts are still 500lbs (1000lbs for both) even though it's going through both flanges.

 

[SwinnyGG]

No.

Think about what would happen in the tug-of-war analogy if one person pulls with 100lb of force and the other person pulls with only 90lb. What's the tension in the rope, and who moves?

 

[Snickster]

Say you attach a rope to a wall on one end and you pull on the loose end with a 1000 pound force. In this case the force in the rope is 1000 pounds. correct? Now instead of attaching the rope to the wall you give it to someone to hold. Now you pull with a 1000 pound force. In order to balance the 1000 pound force you are exerting the other person also needs to pull with a 1000 pound force on the rope but in the opposite direction. correct?

In both cases there is only 1000 pound tensile force in the rope. In the first case the wall provided the opposing force and in the second case the other person provided the opposing force so that in both cases the sum of forces equal zero and no acceleration occured. The force in tensile force of 1000 pounds that was imposed by the person puling was either resisted by the wall or by the other person but still the tensile force in the rope was 1000 pounds.

 

[Snickster]

Another way of stating it is that if you take a cut on the crossection of the rope at any point and if there is static equillibrium there is a 1000 pound force acting in one direction and 1000 pound force acting the the opposite direction on the crossectional area and there is 1000 pounds of tension produced in the rope.

 

[Snickster]

So now take your pressure vessel. You cut the vessel in half and weld the cut end to a steel wall around the entire circumference. You pressurized the vessel to a point where the pressure produces a 1000 pound force internally on the head side acting away from the wall. This 1000 pound force is transfered through the vessel wall, through the weld and then into the supporting wall. On the other side at the wall the pressure force is transferred directly into the wall without going through any part of the vessel. So the tensile force in the vessel wall is 1000 pounds which produses a tensile stress of 1000 pounds divided by the area.

Now remove vessel from wall and reattach the other half by welding the circumferential cut point and pressurize so that there is a 1000 pound force acting on the same end head that was not attached to the wall before. In this case there must be same 1000 force acting on the other end head of the reattached side which balances the other end 1000 pound force thorugh tension in the shell wall.

In any case the net tensile force is only 1000 pounds in the vessel wall.

 

[klliq]

Thanks all! It's just weird thinking that instead of using 4 bolts, that you can use 2 bolts and still have the same force on the bolts.