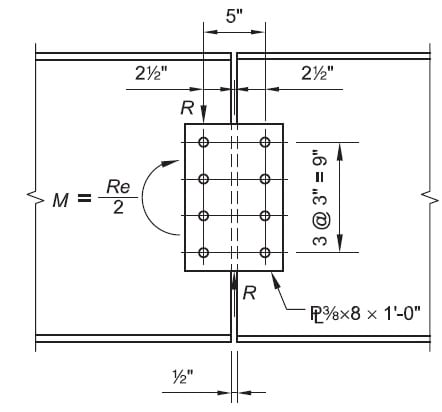
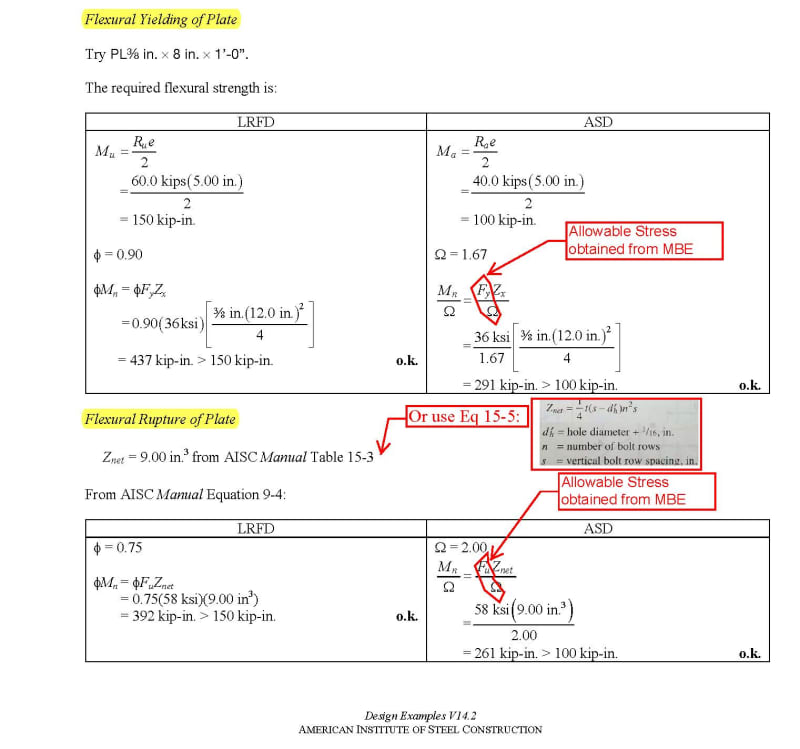
I am involved in a discussion regarding the behavior of a Bolted Web Splice Joint and looking for some clarity to understand the true behavior of the connection.
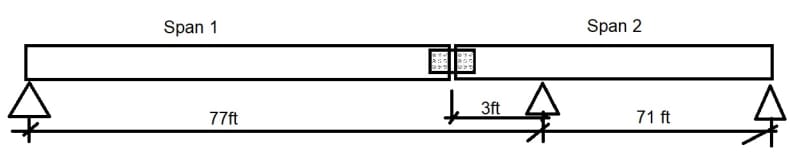
In an existing bridge(several simple spans), one of supports appears to have been constructed incorrectly (shifted by 3ft, whereas all other spans are of the same length). So a Bolted Web Splice Joint is observed in the beams of this span (span1).
Splice detail:
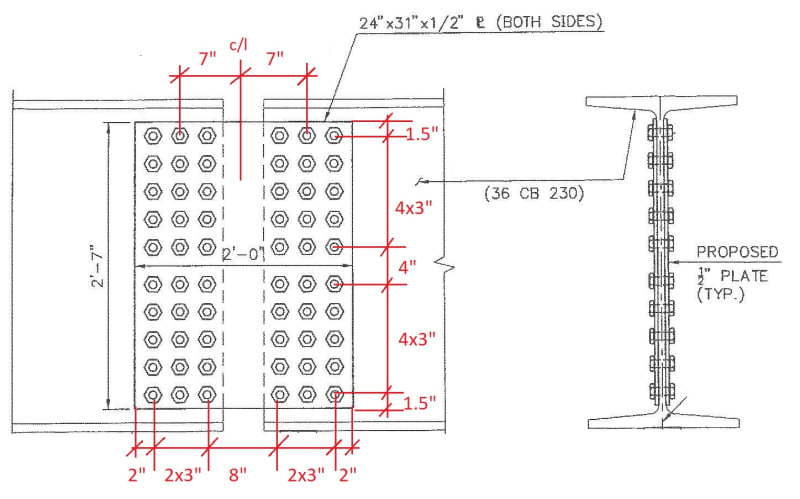
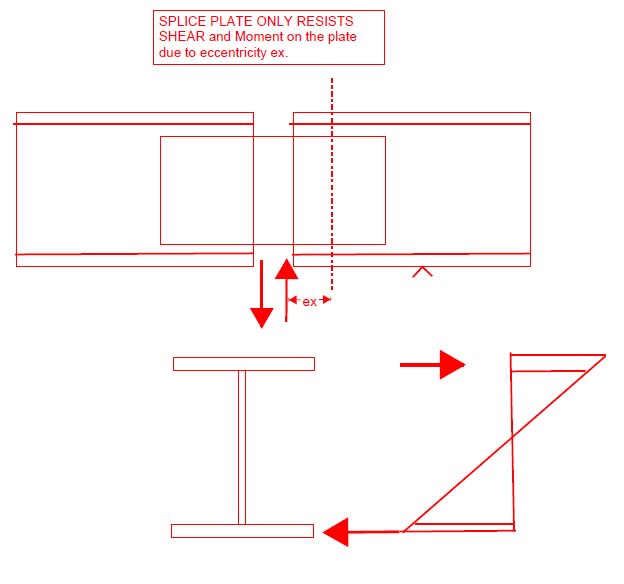
As seen above, there is discontinuity at the top & bottom flanges and the concrete deck above is also discontinuous at this location (expansion joint in deck directly above this splice). Hence it is my understanding that this connection is primarily a shear connection would resist shear and the resultant moment caused by eccentricity of the shear load.
i.e. The span 1 is equivalent of a hung span and the splice connection was never intended to take moment, i.e. the beams were not continuous.
The argument I have received from a colleague is that due to the size of the connection, the rotation of the beams is restricted and hence the behavior will be more like a "partial" moment connection with the system behaving like a 2span continuous beam and the web-splice plate carrying/transferring the bending moment at this location.
I do not agree and feel that flange-splice plates are required to transfer the moment at this connection and a web-splice plate only is not adequate. So I would model the two spans with a "hinge" at the splice location.
Bending moments are primarily transferred through flange splice plates and moment transfer through web portion is not significant. See sketch below:
[ul]
[li]Does the behavior change when you have a connection with so many bolts? Like the bolted connections are locked in with dead load and during live load the beam rotation is prevented thus transferring moment through the web-splice connection?[/li] I can understand this may not be a "pure Hinge" condition, But the moment transfer should not be significant to specifically check the web-splice plate to carry it and if so, what is the expected bending moment? carrying full moment through the connection is not valid. Any thoughts?
[/ul]
In an existing bridge(several simple spans), one of supports appears to have been constructed incorrectly (shifted by 3ft, whereas all other spans are of the same length). So a Bolted Web Splice Joint is observed in the beams of this span (span1).

Splice detail:

As seen above, there is discontinuity at the top & bottom flanges and the concrete deck above is also discontinuous at this location (expansion joint in deck directly above this splice). Hence it is my understanding that this connection is primarily a shear connection would resist shear and the resultant moment caused by eccentricity of the shear load.
i.e. The span 1 is equivalent of a hung span and the splice connection was never intended to take moment, i.e. the beams were not continuous.
The argument I have received from a colleague is that due to the size of the connection, the rotation of the beams is restricted and hence the behavior will be more like a "partial" moment connection with the system behaving like a 2span continuous beam and the web-splice plate carrying/transferring the bending moment at this location.
I do not agree and feel that flange-splice plates are required to transfer the moment at this connection and a web-splice plate only is not adequate. So I would model the two spans with a "hinge" at the splice location.
Bending moments are primarily transferred through flange splice plates and moment transfer through web portion is not significant. See sketch below:

[ul]
[li]Does the behavior change when you have a connection with so many bolts? Like the bolted connections are locked in with dead load and during live load the beam rotation is prevented thus transferring moment through the web-splice connection?[/li] I can understand this may not be a "pure Hinge" condition, But the moment transfer should not be significant to specifically check the web-splice plate to carry it and if so, what is the expected bending moment? carrying full moment through the connection is not valid. Any thoughts?
[/ul]