Boundary condition on a burst pressure test

[assafwei]

I am trying to simulate the following (see image attached): A "box" made of a polymer, the box walls are around 2mm thick and the general dimensions of the box is around 200x200x50mm. The box has 2 nipples one on each side. I am trying to simulate a "burst pressure" test, in reality one of the nipples is capped and the other one is connected via a flexible hose to a pressure source. Since this box is made of a polymer and the walls are not very thick the deformations are substantial (a few millimeters of translation on top and bottom walls), in real life the box might move freely to accommodate for this deformation and I am having a hard time to create boundary conditions that will prevent rigid body motion

 

[jhardy1]

Use the standard "3-2-1" restraint system. Assume xy is the horizontal plane, and z is vertical. Fix z at three nodes on the bottom of the box - three of the corner nodes, say. Now fix x at two of the corners which lie on the y axis, and then add a y restraint to one of those two nodes. All rigid body motions are constrained, but the box is free to "breathe" under application of the loads.

http://julianh72.blogspot.com

 

[rb1957]

I'd suggest using three corners. "all" this does is to establish a plane that the body moves relative to ... so a plane aligned to a face makes "sense".

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[assafwei]

How would I balance the loads if using the 3-2-1 method? The simulation is highly non-linear geometrically and the load balance changes with each step of the solve process.

 

[jhardy1]

Surely the applied load case of internal pressure is self-equilibrating? Upward load equals downward load; longitudinal loads are equal and opposite; lateral loads are equal and opposite.

http://julianh72.blogspot.com

 

[rb1957]

3-2-1 constraints won't react load if your applied loads balance (this is a check of your loading).

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[tigny]

Hello,

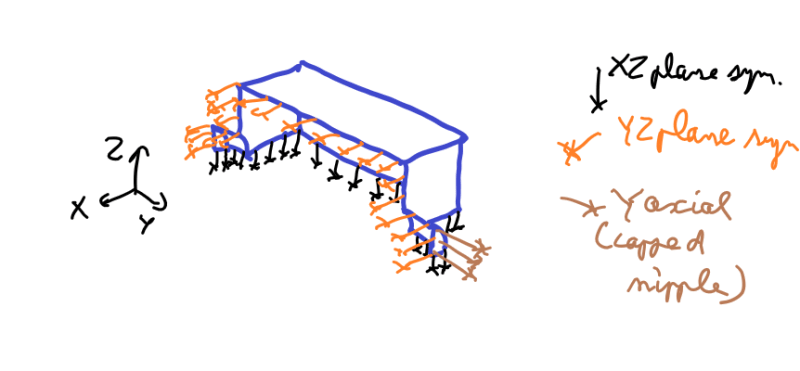
in the vein of 3-2-1; and on order to reduce the calculation cost,
if there are symmetry planes on your box, maybe you could use half or a quarter of your model, therefore some of the rigid modes would be constrained.
You would only need to constrain the axial displacement at the capped nipple.

Pressure would be applied on closed nipples to obtain the equilibrium.

If you don't intend to check buckling nor eingevalues it should be OK.

But maybe buclking is a failure mode for such a thin system?