zrck99
Structural
- Dec 19, 2014
- 82
Hello all,
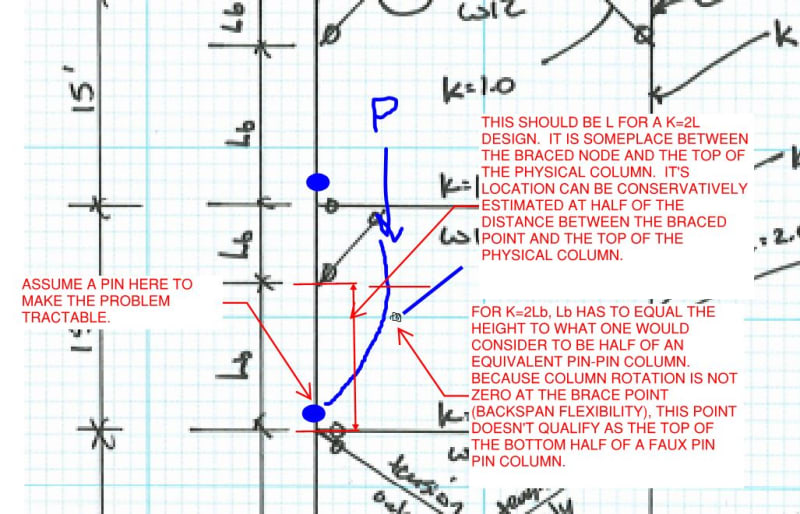
I am designing a 45' tall x 20' wide braced frame shown in the attached pdf. It consists of two knee braced frames above a tension only x brace. I'm hoping that someone can either confirm my assumptions for k factors or point me in the right direction for correcting them. My columns will be continuous from the ground to the top of the full frame. Each beam and brace member is hinged at each end.
My understanding is that at the x brace, we can use a k = 1 for the beam and column because this frame is non sway so worst case k = 1 and by running the column on up past the x brace level, we would be adding some fixity and the resulting k would be reduced from 1.0 some.
When I have modeled single story knee braces in the past, I've considered the bottom of the column to be a pin and the upper brace to create fixity resulting in a k = 2.0 and unbraced length = the height from the ground to the knee brace work point or the distance from the knee brace work point to the top of the column. In a case like I have shown with the columns continuous from the ground to the top of the frame, does this cause the k factor to decrease to something below 2 because we have some added fixity at the node just above the x brace rather than a pin/hinge?
Lastly, I'm considering the beams pinned at each end with a k = 1.0.
Any thoughts?
Thanks,
ZRC
I am designing a 45' tall x 20' wide braced frame shown in the attached pdf. It consists of two knee braced frames above a tension only x brace. I'm hoping that someone can either confirm my assumptions for k factors or point me in the right direction for correcting them. My columns will be continuous from the ground to the top of the full frame. Each beam and brace member is hinged at each end.
My understanding is that at the x brace, we can use a k = 1 for the beam and column because this frame is non sway so worst case k = 1 and by running the column on up past the x brace level, we would be adding some fixity and the resulting k would be reduced from 1.0 some.
When I have modeled single story knee braces in the past, I've considered the bottom of the column to be a pin and the upper brace to create fixity resulting in a k = 2.0 and unbraced length = the height from the ground to the knee brace work point or the distance from the knee brace work point to the top of the column. In a case like I have shown with the columns continuous from the ground to the top of the frame, does this cause the k factor to decrease to something below 2 because we have some added fixity at the node just above the x brace rather than a pin/hinge?
Lastly, I'm considering the beams pinned at each end with a k = 1.0.
Any thoughts?
Thanks,
ZRC