nivoo_boss
Structural
- Jul 15, 2021
- 132
Hey everyone!
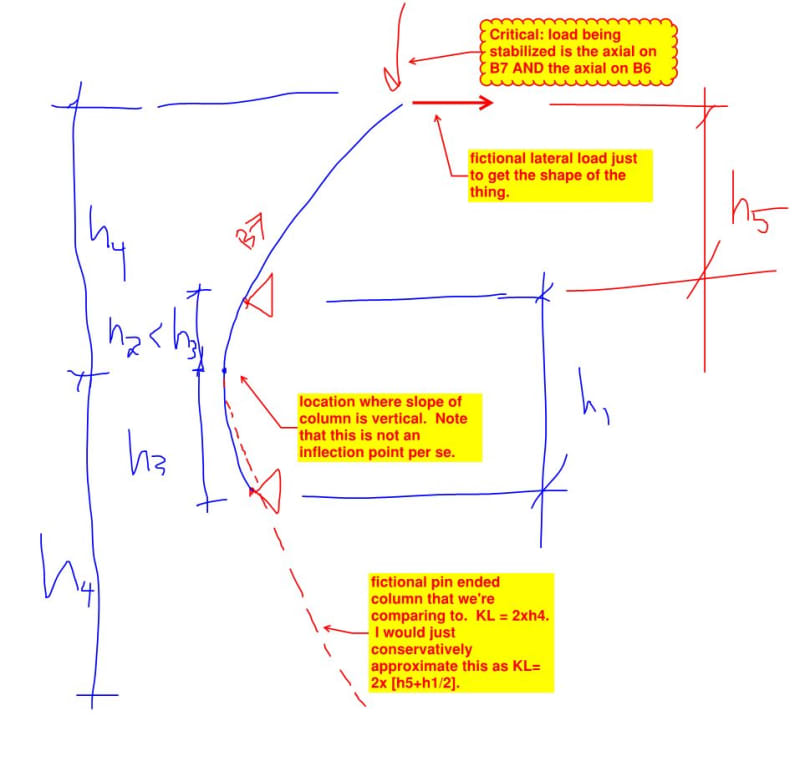
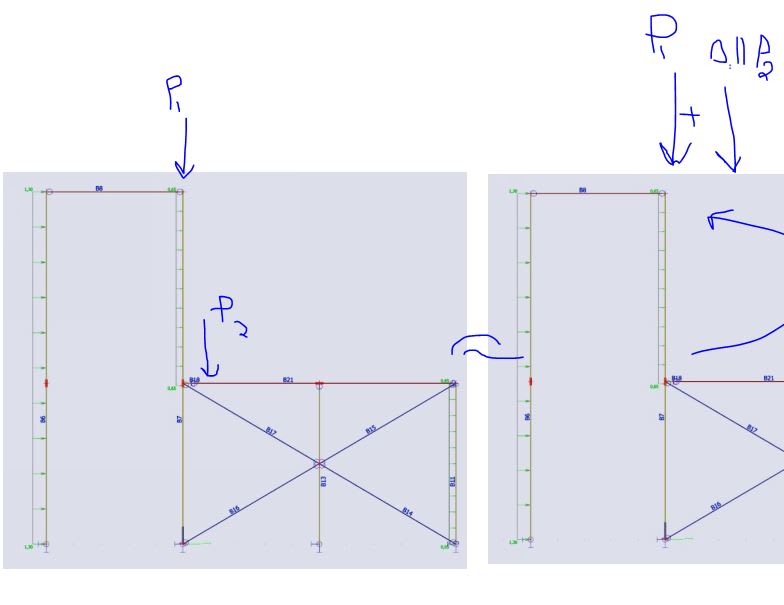
What the buckling lengths for member B6 and the top half of B7 should be? All supports are pinned and currently connections between the beam B8 and its columns are pinned as well. B6 is about 13 m high.
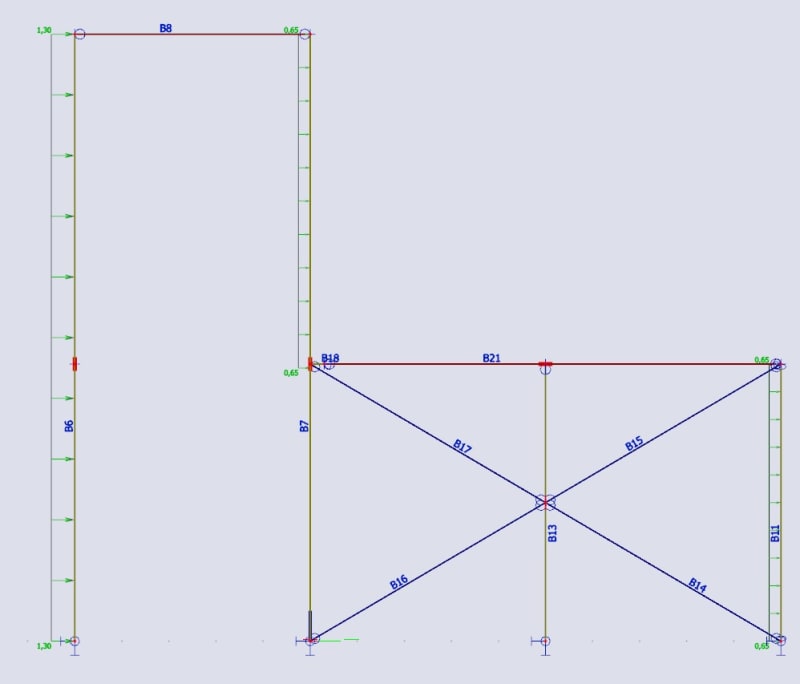
What the buckling lengths for member B6 and the top half of B7 should be? All supports are pinned and currently connections between the beam B8 and its columns are pinned as well. B6 is about 13 m high.