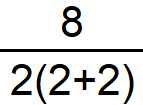Burunduk and 3DDave math problem

[greenimi]

3DDave and Burunduk,

Probably you won't agree with each other on what is the "correct" result of

8:2(2+2)

I am not taking sides just curious of your answers, if you will.
Is it 1?
Is it 16?

Probably that's why PEMDAS exist in the first place.

"Failing to understand the general principle of multiplication vs. addition" is indicated when someone suggests that the solution of 2 X 3 can be thought to be 5 only because 2 + 3 equals 5.
Understanding what is multiplication, and how there is no multiplication without addition, is when someone gets the idea that the solution for 2 multiplied by 3 is the sum of 2 added to 2 and then another 2 added. Unfortunately, some don't get even this simple concept. They should finally learn what they should have in elementary school, like basic math operations and stuff like what an analogy is (to understand how an analogy that demonstrates an idea related to a topic is drawn by bringing an example from a different topic).

 

[Belanger]

"Probably won't agree with each other..."
Understatement of the year

John-Paul Belanger
Certified Sr. GD&T Professional
Geometric Learning Systems

 

[Burunduk]

The answer is 16.
Parentheses first, then from left to right.
It would be 1 had the expression been written as 8:[2(2×2)]

 

[Burunduk]

BTW, "there is no multiplication without addition" has a specific context in the thread you quoted that from.
It shouldn't be interpreted as a general standalone statement. It's not true as such.

 

[greenimi]

Burunduk,

I agree with what you concluded and your answer (16), but (and it's always a but) that are other camp of people who interpret the expression I wrote above ---- 8:2(2+2)----
as

and it is not definitive answer (because it is left intentionally ambiguous) on which interpretation should/ could be used.

That’s why I agree with you that adding parentheses will solve the conundrum, although I haven’t added them (intentionally)

My point is, if we don't agree on this simple math problem, how do you expect to agree on an even more complex issues regarldess if it GD&T interpretation or anything else in the world......

 

[3DDave]

The error was what would result if the insistence on what a special case seemed to produce was used in a different context. Burunduk took it out of context. The context was that special case of scalar addition of two arguments happened to equal to the scalar multiplication of the same two arguments; that an offset looks like a translation, when the two operators are functionally different.


As to this math problem - that's what RPN or postfix notation is intended for, which is how numerical processors work. PEDMAS is workaround to produce an agreed upon algebraic interpretation where the order of application is otherwise ambiguous. There are applications that take arguments purely left-to-right which produce a different result than PEDMAS.

Post-fix:

8
2
2
+
2
/
*
is one way that would be put to the stack.

8
2
2
2
+
/
*
would also work.

 

[greenimi]

3DDave,

Regarding the math problem, I am afraid I am not understanding your last replay.
Just for my own knowledge, could you, please, explain it?

What means:

Post-fix:

8
2
2
+
2
/
*
is one way that would be put to the stack.

8
2
2
2
+
/
*
would also work.

?

 

[3DDave]

Crap - got the second on backwards. The first one:

[pre]
8 2 2 + 2 / *
^ (take the preceding two 2s and the plus and replaces with 4
8 4 2 / *
^ (take the preceding 4 and divide by the 2 and replace with 2
8 2 *
^ (take the preceding 8 and multiply by the 2 and replace with 16
16
[/pre]

The second one requires an EXCH (exchange operator to swap the order of arguments. It's been 20+ years since the last time, so I'm rusty.

8 2 2 2 + EXCH / *
[pre]
8 2 2 2 + EXCH / *
^ ((take the preceding two 2s and the plus and replaces with 4)
8 2 4 EXCH / *
^ ( Exchange the 2 with the 4
8 4 2 / *
^ (take the preceding 4 and divide by the 2 and replace with 2
8 2 *
^ (take the preceding 8 and multiply by the 2 and replace with 16
16
[/pre]

Some implementations use "SWAP" instead of EXCH; In Postscript postfix the math operators are "add", "mul", "div", and "sub"

In all cases the formula is evaluatated from one end, with numbers being skipped until an operator is encountered. The operator does it's function, removing the arguments, if any, from the stack, and the result, if any, is placed on the stack in its place.

 

[CheckerHater]

There are applications that take arguments purely left-to-right which produce a different result than PEDMAS.

I didn't realize that you don't have to go far to find such "applications".

Open Windows Calculator and enter "2 + 2 * 2 =" in "normal" and "scientific" modes.

"For every expert there is an equal and opposite expert"
Arthur C. Clarke Profiles of the future