Calculate J and Cw for W Section 6

[dik]

Does anyone have formulas for calculating J and Cw, Torsional Constant and Warping Constant given b, h, t, and w? Also if someone has formulae for J and Cw for a W section with plates welded across the toe of the flanges? Thanks in advance.

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[Agent666]

Do you need to account for the root fillets accurately? Or are you after an approximate estimate?

How accurate do you need to be is the question?

 

[GregLocock]

Torsional constants for open sections are very difficult to work out accurately by hand. The quickest way is usually FEA. Plane sections don't remain plane, and all that sort of fun.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[dik]

Within 5% or 10% is great... I've already used the approx values in the steel handbook for the properties.


Out of the question... way too refined... as a guess, I've used an HSS 6x6x5/16 for torsional properties... close enought, I suspect and has a stiffener in the middle...Column is a W6x15.5 and have used BAR 3/8x7 reinforcing across the toes...

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[robyengIT]

I don't know them very well : hope it can help

 

[robyengIT]

Dik : like this (italian - metric)?

 

[Settingsun]

Is this it? From CISC

https://www.google.com/url?sa=t&sou...FjABegQIBBAI&usg=AOvVaw2UOG2bpaylcXTs7OhJeT5f

Also here for just J:

https://deepblue.lib.umich.edu/bits...8/bab4733.0001.001.pdf?sequence=5&isAllowed=y

 

[r13]

dik,

See CH-3 (on p.7) of AISC DG-9. The formula are there.

 

[robyengIT]

with ref. AISC DG 9 I found this excel program

 

[dik]

I want to reinforce it like

Client has building with 18' high W6x15.5 columns and wants to add a 1000 lb jib crane to one... and it needs reinforcing. Plan to plate the column affected as shown...

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[r13]

I don't think there is exact reference. Try these formula. For J, I would sum the parts - J_W+ J_PL.

 

[dik]

Thanks guy... attached SMath file...

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[dik]

and another...


Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[r13]

dik,

Here is C_W for closed section (the previous one is for open shapes).

 

[Agent666]

Those formulae for the I section are the ones I was thinking of. But they are of course quite approximate which is why I wanted to know how accurate you wanted to be.

There is a solution by Darwish & Johnson paper from 1964 for the torsion constant that allows for accounting for the root fillets. It seems to have been replicated over the years in a few other publications, but they never seem to express the limits on some of the section parameters form this original paper (though having said that even when you are outside the limiting ratios it still gives a closer answer to the true value than the plain old 1/3*sum(b*t^3) formula).

I'm not aware of any similar formulas for accounting for the root fillets for determining the warping constant.

Once you're into the plates on the side you've created a closed section, and the I section formulas can no longer be applied. A FEM solution is the only real way to get an accurate result here. Sure you could maybe estimate it using the closed section formula r13 pasted above any ignore the projections past the flange tips and ignore the web. But I find it hard to imagine it will be anywhere near 5-10% of the true answer.


If you're after a free FEM solution try this python package, there are plenty of examples in the docs to get you started. But I'll post an example file shortly that provides a solution to the plates on the side option that you can play around with. Change the inputs as required. Alternatively if you have a test scenario I can run it for you to compare to your estimates. Will post back soon once I've written the code.

 

[dik]

Thanks guys/gals... got it...

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[dik]

Since it's almost a closed section... I'll use a closed section calc to see how it compares to the HSS 6x6 I already used for comparison... noting that it's 44ksi material and not 50ksi stuff... Thanks, you've been a lot of help.

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[Agent666]

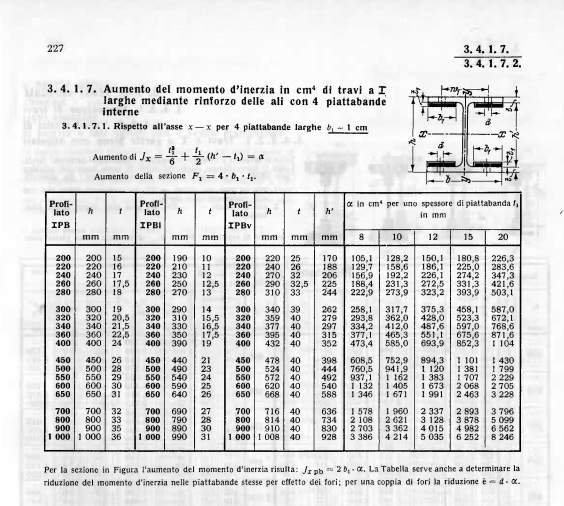
import sectionproperties.pre.sections as sections
from sectionproperties.analysis.cross_section import CrossSection

mesh_area = 25  # max mesh size

d = 612  # I section depth
b_f = 229  # I-section flange width
t_f = 19.6  # I-section flange thickness
t_w = 11.9  # I-section web thickness
r_1 = 14  # I-section root radii
n_r = 50  # number of points considered around root radii

d_p = 650  # strengthening plate depth
b_p = 12  # strengthening plate thickness

# create constituent geometry
geometry1 = sections.ISection(d=d, b=b_f, t_f=t_f, t_w=t_w, r=r_1, n_r=n_r, shift=[-b_f / 2, -d / 2])
geometry2 = sections.RectangularSection(d=d_p, b=b_p, shift=[-b_f / 2 - b_p, -d_p / 2])
geometry3 = sections.RectangularSection(d=d_p, b=b_p, shift=[b_f / 2, -d_p / 2])

# create merged section
geometry = sections.MergedSection([geometry1, geometry2, geometry3])

# add holes
geometry.add_hole([-b_f / 3, 0])
geometry.add_hole([b_f / 3, 0])

# create mesh
mesh = geometry.create_mesh(mesh_sizes=[mesh_area, mesh_area, mesh_area])

# clean geometry
geometry.clean_geometry(verbose=True)

# create section
section = CrossSection(geometry, mesh)

# calculate results
section.calculate_geometric_properties()
section.calculate_plastic_properties()
section.calculate_warping_properties()

# plot results
section.plot_mesh()
section.plot_centroids()

# display all results
# check [URL unfurl="true"]https://sectionproperties.readthedocs.io/en/latest/rst/post.html[/URL] for definitions
section.display_results(fmt='.3f')

# this will specifically display torsion and warping constants
J = section.get_j()
I_w = section.get_gamma()
print(f'J = {J}')
print(f'I_w = {I_w}')

Or download the python script here.

Let me know if you want me to run a specific scenario for comparison with your estimates? Will be interesting to see how accurate you think you're being? Whether the accuracy really matters is another thing....

 

[r13]

I agree that your section is a two cells closed box. The formula for open section is not appropriate. Here is the formula for closed box section, however, note the b/t ratio limitation. So far I failed to find J for closed box shape with thick walls. The general form of this formula is J = 4A_P²/Σ(l_i/t_i), A_P is defined in article below, Σ(l_i/t_i) is summing length/thickness ratio of all sides forming the closed box section. You need to get the torsional constant for a single cell, then multiply by 2. But I am not aware how to handle the double counting on the web though.

 

[Settingsun]

you could maybe estimate it using the closed section formula r13 pasted above any ignore the projections past the flange tips and ignore the web. But I find it hard to imagine it will be anywhere near 5-10% of the true answer

Iw is usually taken as zero for closed sections, and the central web and plate outstands shouldn't contribute significantly to J. Let's see what python says.