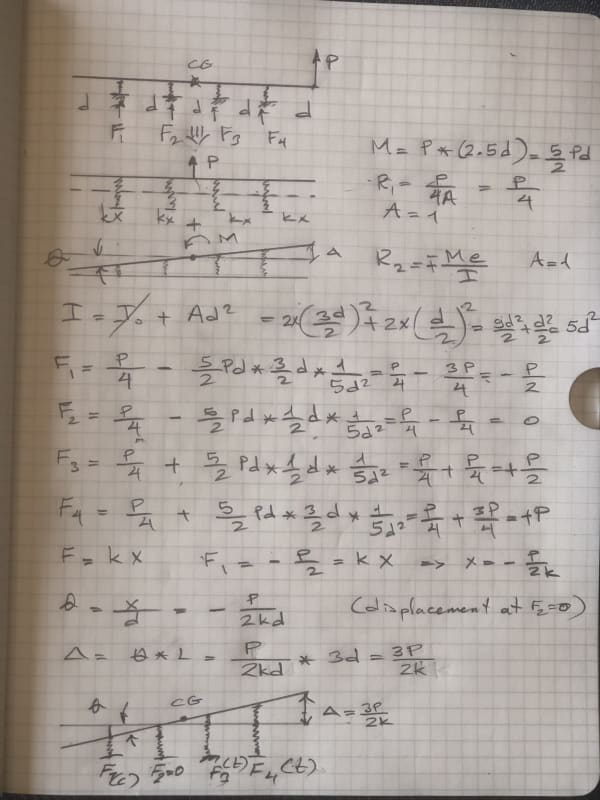engtiuser2 (Mechanical)(OP) said:
2nd line: Assuming R1 is the upward force at first support created by P, should it be simply P/4? Not sure why A is involved.
4th line: The equation looks familiar (like bending stress formula). Can you explain how is it applicable to the beam under rigid body rotation? A link to website with this equation application is helpful.
5th line: It would be nice if I can see where is the axis of the second moment of area (I) and the area. The I in the bending moment equation is for the cross section of the beam, can you explain how line 5 arrived....
We are at different time zones..I think it is clear, the transfer of force ( P ) to C.G. with Moment M=2.5d* P
The superposition is applied, assuming the beam is rigid.
2nd line = The vertical force P is resisted by four springs . You are right... Eventually Fi= P/4
Famous bending formula is applied : f= P/ΣA +,- (M*y/I) this formula is used to obtain stresses.
In order to find the forces , a similar formula adopted, Fi= P/n +,- (M *y/It)
Assuming identical springs , The force for each spring will be Fi =P/4
4th line: The equation looks familiar (like bending stress formula). Can you explain how is it applicable to the beam under rigid body rotation? A link to website with this equation application is helpful.
The inertia of 4 springs about C.G. is calculated using parallel axis theorem I= Io + A*d**2 Io is zero and area is 1 for this case ,
It=Σ A**d2
5th line: It would be nice if I can see where is the axis of the second moment of area (I) and the area. The I in the bending moment equation is for the cross section of the beam, can you explain how line 5 arrived....
Second moment of 4 springs about C.G. It= 5d**2
And the total area Σ A = 4 (there are 4 springs ).
The same approach is applied to find the resisting forces of each pile under a rigid pile cape. I write (force distribution under a rigid pile cap pdf ) searched the web . one of the link is below...just read page 7 and following pages...
file:///C:/Users/user/Downloads/Two%20Pile%20Group.pdf