Calculation of chart data - Column Design - concrete - Biaxial bending 2

[Pretty Girl]

This is from "Reinforced concrete design to eurocodes" by prab bhat, page 371.

I have two things which I'm confused of.

1:
I'm bit confused of how did they assumed (chose) the alpha = 2 and beta = 1.5 for the first line? Why not something like alpha = 2.1 and beta = 1.4.

If they used random data (2 and 1.5) with even slight variations like alpha = 2.1 and beta = 1.4, then the axial force and moments would render a different result.

So what is the reason of that choice. It can't be random, or can it?

2:
Further, don't we need the My/b2h table as well to have a combined chart?
or this mx is used as a seperate chart and then for My, another chart is being used to design the other axis seperately?

 

[HTURKAK]

So what is the reason of that choice. It can't be random, or can it?

These are randomly selected to start with ,but you should select different α and β to locate NA so to cover the total cross-section and draw the chart with reasonable accuracy.

2:
Further, don't we need the My/b2h table as well to have a combined chart?
or this mx is used as a seperate chart and then for My, another chart is being used to design the other axis separately?

The Fig. 9.22 Column design chart for axial force and biaxial bending is valid for My/b2h=2.0 only. Total biaxial bending graph is 3D like bulb.
The following excerpt from NARAYANAN , Design of RC Structures.



Notice that Case (a) , My =0 and Case (b) Mx= 0 , these are unique and uniaxial bending while Case (c) biaxial and there can be a lot of different cases.

 

[Pretty Girl]

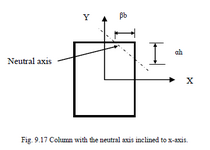
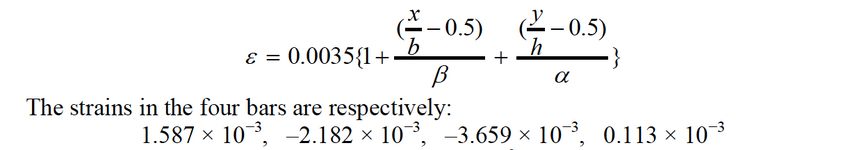These are randomly selected to start with ,but you should select different α and β to locate NA so to cover the total cross-section and draw the chart with reasonable accuracy.





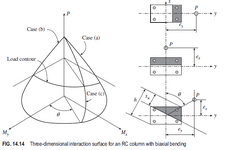
The Fig. 9.22 Column design chart for axial force and biaxial bending is valid for My/b2h=2.0 only. Total biaxial bending graph is 3D like bulb.
The following excerpt from NARAYANAN , Design of RC Structures.
View attachment 2420


Notice that Case (a) , My =0 and Case (b) Mx= 0 , these are unique and uniaxial bending while Case (c) biaxial and there can be a lot of different cases.

@HTURKAK
Thank you for the response.

So, that means the method in the book cannot be used for real life design of columns. That method is not accurate?

Why can't we separately produce two charts for each axis than using a "bulb" like graph?
I mean, we already know how much maximum strain a specific steel bar goes through, and the contribution ratio for each axis (eg: -0.230, -0.315, for the bar 1) (the method in that book).



Then why can't we just use one of the contribution ratios (let's say we chose -0.230 for x axis), then calculate the new maximum strain for that specific bar for x axis, and produce a chart by considering it as a uni-axial column. And then do the same for other contribution ratio -0.315 and produce a chart with it. Then we will have two seperate charts for each axis, but fully compatible for bi-axial design of column. Is that incorrect or unsafe method for real life situations?

eg:
contribution for X axis -0.230
contribution for Y axis -0.315

summation of those = -0.545

and for that yield strain of steel for that steel bar (ε) = 1.587 x 10^-3 (the answer in that book for the bar 1)

the x axis contribution's percentage if we calculate it,(-0.230 / -0.546)*100 = 0.422%,
then why can't we just calculate following from that
(1.587 x 10^-3) * 0.422 =0.00067 as the new strain for x axis and design it as uniaxial chart? (and then we shall repeat the same calculation for other axis to produce a seperate chart for that axis)

Any suggestions to produce an accurate bi-axial charts (two seperate charts is fine if it's accurate) than using a bulb?, which is not practical if not using software.

I feel like entire calculation of biaxial bending of this prab bhat's book is an approximate method not an accurate method, as even the contributions feels like not correct in that book and feels like it assumed that the neutral axis always occur perpendicular to an axis. Which is not correct, is it?

What if we already know the Mx/My ratio? then the book's method is accurate for real-world calculations?
Because we always have that Mx and My before designing the column anyways. Let's say Mx = 200 kNm and My = 50 kNm, so the ratio is 200/50 = 4:1. So we can simply use that ratio for beta and alpha?

eg:

beta | alpha
4 | 1
8 | 2
16 | 4

and then produce the chart to have an accurate chart for that specific Mx = 200 kNm and My = 50 kNm case?

I don't actually want to produce a universal chart. I just need to have a chart to design a column if we know the N, Mx and My. As my applications are real-world.

 

[HTURKAK]

So, that means the method in the book cannot be used for real life design of columns. That method is not accurate?

Why can't we separately produce two charts for each axis than using a "bulb" like graph?
I mean, we already know how much maximum strain a specific steel bar goes through, and the contribution ratio for each axis (eg: -0.230, -0.315, for the bar 1) (the method in that book).

The method ( The column capacity for biaxial moments ,the three-dimensional interaction failure surface ),AFAIK the method used at design softwares .( I know e.g . SAP 2000 uses Biaxial Interaction Surfaces ) still the most precise method.

But for manual calculation,
- Follow EC-2 Bresler's formula or ,
- BS method , equivalent moment in one of the axes if applicable.
The following snippet from INTRODUCTION TO EUROCODE 2 ,Design of concrete structures , By Derrick Beckett..

 

[Pretty Girl]

The method ( The column capacity for biaxial moments ,the three-dimensional interaction failure surface ),AFAIK the method used at design softwares .( I know e.g . SAP 2000 uses Biaxial Interaction Surfaces ) still the most precise method.

But for manual calculation,
- Follow EC-2 Bresler's formula or ,
- BS method , equivalent moment in one of the axes if applicable.
The following snippet from INTRODUCTION TO EUROCODE 2 ,Design of concrete structures , By Derrick Beckett..

View attachment 2445

Thank you for the book reference, I'll go through it and thank you for the explanation provided.

So, this is the most accurate method, as you mentioned? "The column capacity for biaxial moments ,the three-dimensional interaction failure surface".

Are there any books that contain the step by step calculation from the beginning (cases 1- 4) and finally come up with the 3d interaction failure surface?. It's alright if it's excessively lengthy (lengthier is better as it would contain every step). I want to learn how to do it properly (as I don't like approximations and less accurate methods).