Batzo
Civil/Environmental
- Apr 21, 2020
- 46
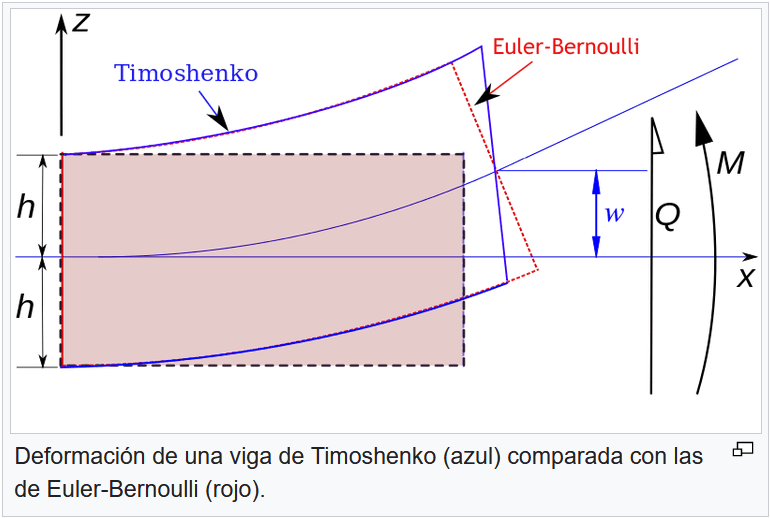
Why for a cantilever (fixed-free beam) with a point load at the end,
the cross section rotations are equivalent between a Timoshenko and Euler Bernoulli Beam?
the cross section rotations are equivalent between a Timoshenko and Euler Bernoulli Beam?

![[surprise] [surprise] [surprise]](/data/assets/smilies/surprise.gif)