Kedu
Mechanical
- May 9, 2017
- 193
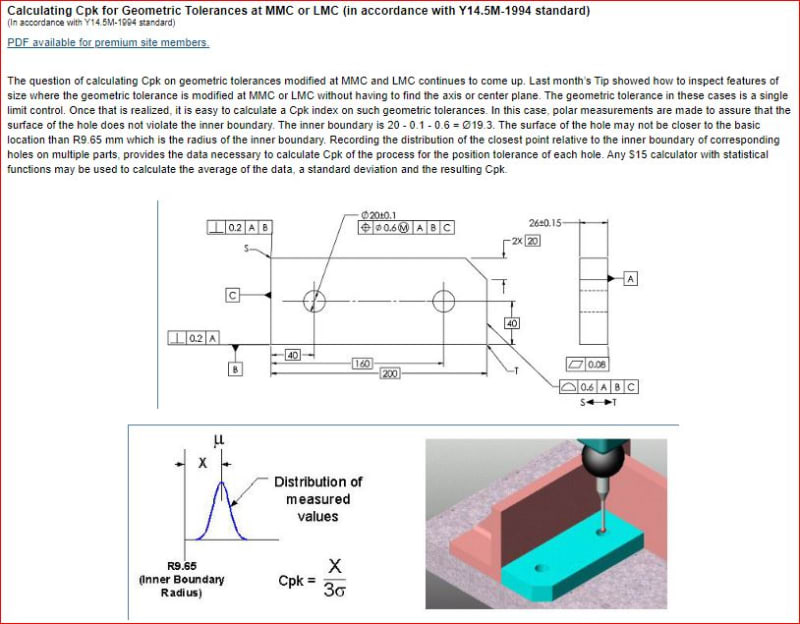
Does anyone know (or maybe has an article to post) on how to do a capability study on position tolerance at MMC callout using "Virtual Condition" boundary approach?
As far as I remember, and read, this method has been developed (and shown) by prof. Don Day few years ago.
Few questions came in my mind:
- is the capability study done on "the combo" size and position instead of position alone?
- in order to use known Cp, Cpk formulas, do size and position should be independent?
- is feature's size variation taken in consideration when "VC boundary" method used?
As far as I remember, and read, this method has been developed (and shown) by prof. Don Day few years ago.
Few questions came in my mind:
- is the capability study done on "the combo" size and position instead of position alone?
- in order to use known Cp, Cpk formulas, do size and position should be independent?
- is feature's size variation taken in consideration when "VC boundary" method used?