cr7
Automotive
- Dec 21, 2019
- 65
Hi guys,
looking at 5459:2011 I would like to be sure, would the DRF (center plane) be exactly the same in both callouts?
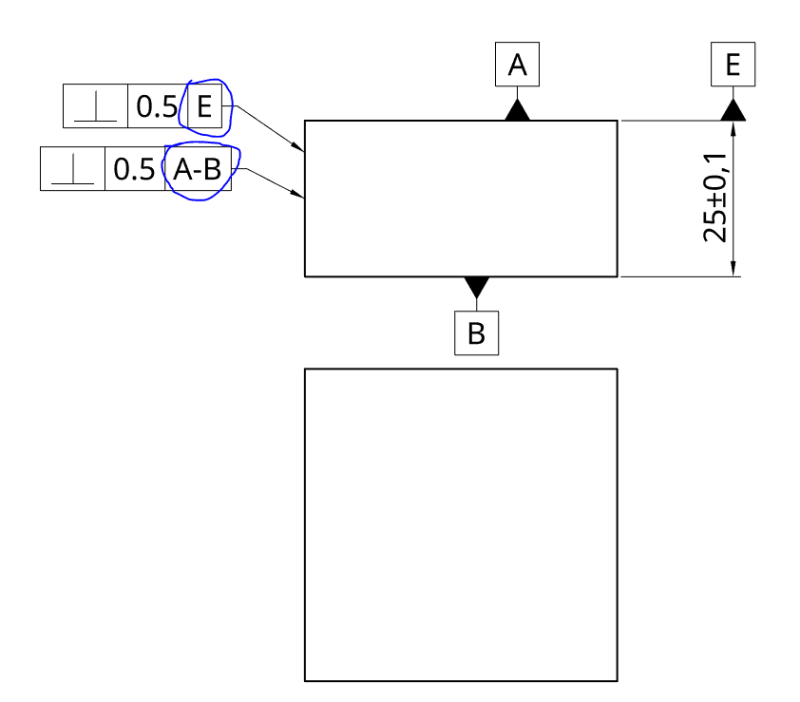
looking at 5459:2011 I would like to be sure, would the DRF (center plane) be exactly the same in both callouts?

