MTSOE
Structural
- Aug 25, 2023
- 29
Hello.
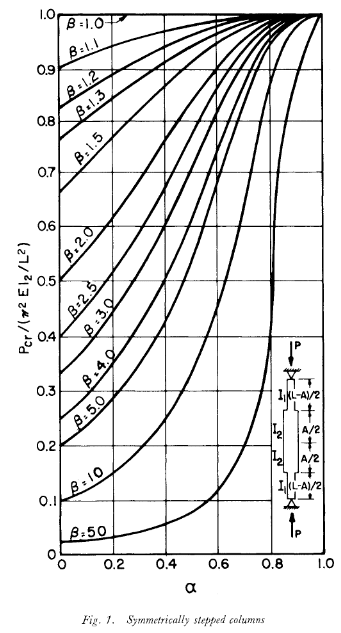
My company designs support of excavation and often incorporates steel pipe struts/corner braces. These members consist of pipe with pieces of wide flange slotted into the ends of the pipe. The purpose of the wide flange sections is to create a better welded connection to the vertical piles. Recently, a contractor accidentally cut a piece of pipe too short and asked if they could make up the length with longer wide flange sections. We told them to get a new piece of pipe and build what's on the drawings. But I was left wondering, how long could the wide flange sections be? Typically, we only check the axial capacity of the pipe and the weak axis buckling of the wide flange is ignored given the short span. But how would I go about checking a variable cross section compression member? I've found some papers on "stepped columns" and some useful formulas in Roark's Stress and Strain but I feel like a simpler check is eluding me. Does anyone have any ideas? I've attached a photo of a similar corner brace for your reference. Thanks

My company designs support of excavation and often incorporates steel pipe struts/corner braces. These members consist of pipe with pieces of wide flange slotted into the ends of the pipe. The purpose of the wide flange sections is to create a better welded connection to the vertical piles. Recently, a contractor accidentally cut a piece of pipe too short and asked if they could make up the length with longer wide flange sections. We told them to get a new piece of pipe and build what's on the drawings. But I was left wondering, how long could the wide flange sections be? Typically, we only check the axial capacity of the pipe and the weak axis buckling of the wide flange is ignored given the short span. But how would I go about checking a variable cross section compression member? I've found some papers on "stepped columns" and some useful formulas in Roark's Stress and Strain but I feel like a simpler check is eluding me. Does anyone have any ideas? I've attached a photo of a similar corner brace for your reference. Thanks