aniiben
Mechanical
- May 9, 2017
- 158
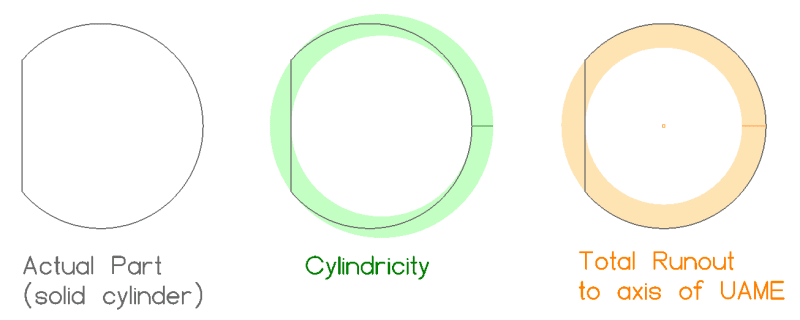
I read some discussions about self-referencing runout (circular and total) and I'm trying to understand why cylindricity could be considered "equal" to "self- referencing" total runout, but not the same thing could be said about circularity and circular runout.
No practical application. Just purely academic and theoretical discussion.
Also, I agree that "self referencing" should be avoided to eliminate any misinterpretation and inspection problems that must be overcome with non classical inspection techniques.
From different thread copy-paste:
"I agree that in case of total runout it would be equal to cylindricity, however for circular runout I think it is different from circularity and in certain, though very untypical, situations it may make sense. And I also agree that standard approach is to use runout for controlling feature(1)-to-feature(2) relationship, and not "runout being used on a single feature with a single self-referencing datum". " end of copy-paste.
No practical application. Just purely academic and theoretical discussion.
Also, I agree that "self referencing" should be avoided to eliminate any misinterpretation and inspection problems that must be overcome with non classical inspection techniques.
From different thread copy-paste:
"I agree that in case of total runout it would be equal to cylindricity, however for circular runout I think it is different from circularity and in certain, though very untypical, situations it may make sense. And I also agree that standard approach is to use runout for controlling feature(1)-to-feature(2) relationship, and not "runout being used on a single feature with a single self-referencing datum". " end of copy-paste.

![[wink] [wink] [wink]](/data/assets/smilies/wink.gif)
![[bow] [bow] [bow]](/data/assets/smilies/bow.gif) , but I am trying to fully get your point of view about circularity.
, but I am trying to fully get your point of view about circularity. ![[thanks2] [thanks2] [thanks2]](/data/assets/smilies/thanks2.gif)
![[upsidedown] [upsidedown] [upsidedown]](/data/assets/smilies/upsidedown.gif) I should have known you had your reasons and wouldn't have missed something like that - I had a feeling as such after I posted my reply.
I should have known you had your reasons and wouldn't have missed something like that - I had a feeling as such after I posted my reply.