Gradstructengineer
Structural
- Sep 13, 2022
- 10
Hi All,
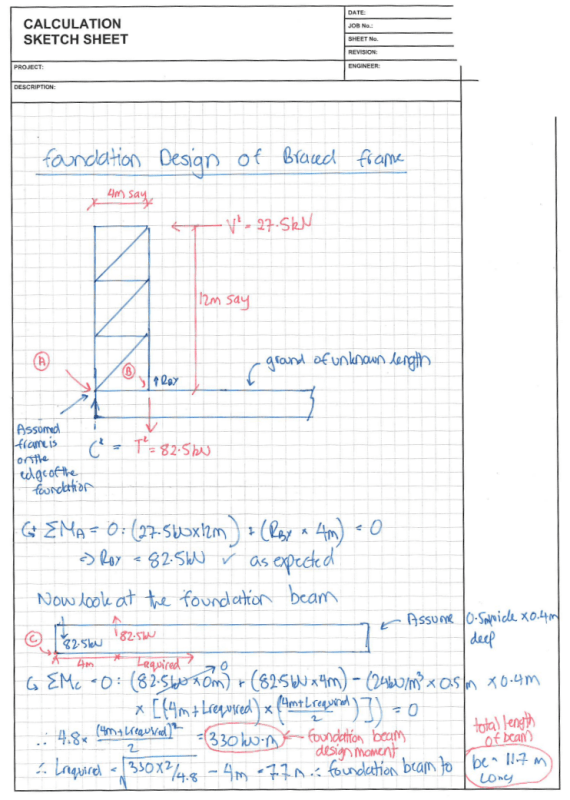
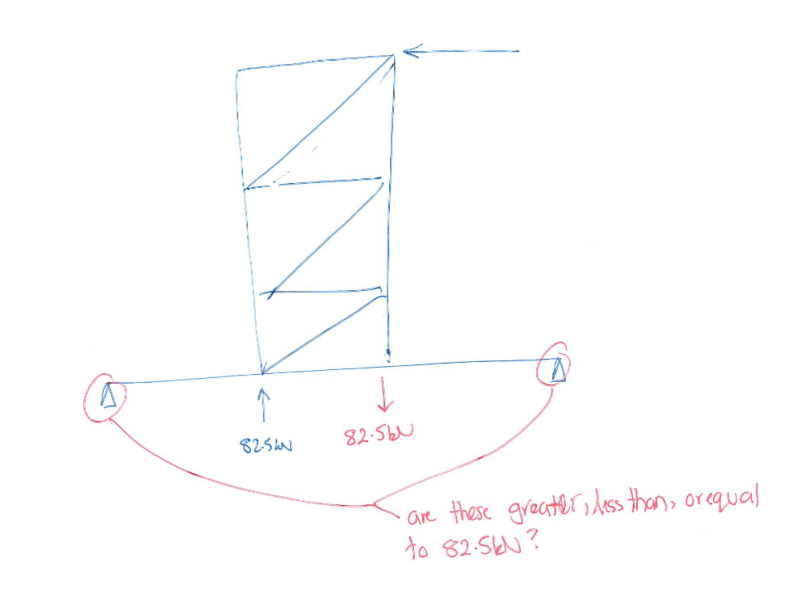
I have to design the footing for a truss brace. Please see attached image. Under wind loading the support reactions at the base of the footing are 82kN and -82.5kN. Do these forces cancel out each other with the total uplift load as 0.5kN or do I need to design a footing with a SW of 82.5kN to sustain the uplift forces of 82.5kN?
thanks in advance
I have to design the footing for a truss brace. Please see attached image. Under wind loading the support reactions at the base of the footing are 82kN and -82.5kN. Do these forces cancel out each other with the total uplift load as 0.5kN or do I need to design a footing with a SW of 82.5kN to sustain the uplift forces of 82.5kN?
thanks in advance