Lutfi
Structural
- Oct 20, 2002
- 1,036
It has been a long while since I have been in this forum. Hello everyone.
I want to pick everyone’s brain here.
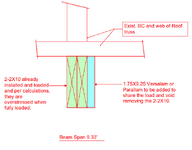
I have been called, of course after the fact, to evaluate a situation where a contractor has already installed a beam, 9.33’ span made up from SYP number 2. The beam is supporting 5 roof trusses, and it is already loaded. See the attached simple and NTS section.
The contractor and the owner are not for removing and replacing the already installed 2-2X10.
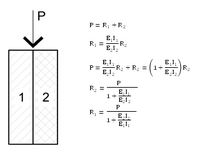
My approach is to add an Microlam on one side or both sides of the beam. I know the conservative approach is to assume the Microlam will carry all the entire load. This would be the easy way out. However, being an engineer, I want a logical way that I can use with the assumption that both beams are sharing the load proportionally based on their stiffness. So, I can apply prorated load to each one.
My question is, how to come up with a logical prorating percentage?
Please no comment to chastise the contactor nor the owner.
I want to pick everyone’s brain here.
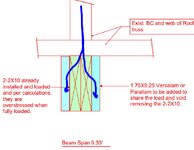
I have been called, of course after the fact, to evaluate a situation where a contractor has already installed a beam, 9.33’ span made up from SYP number 2. The beam is supporting 5 roof trusses, and it is already loaded. See the attached simple and NTS section.
The contractor and the owner are not for removing and replacing the already installed 2-2X10.
My approach is to add an Microlam on one side or both sides of the beam. I know the conservative approach is to assume the Microlam will carry all the entire load. This would be the easy way out. However, being an engineer, I want a logical way that I can use with the assumption that both beams are sharing the load proportionally based on their stiffness. So, I can apply prorated load to each one.
My question is, how to come up with a logical prorating percentage?
Please no comment to chastise the contactor nor the owner.