Hello,
I have spent a couple of days fruitlessly searching forums for the answer, but I haven't found it yet so I thought I was ask it here.
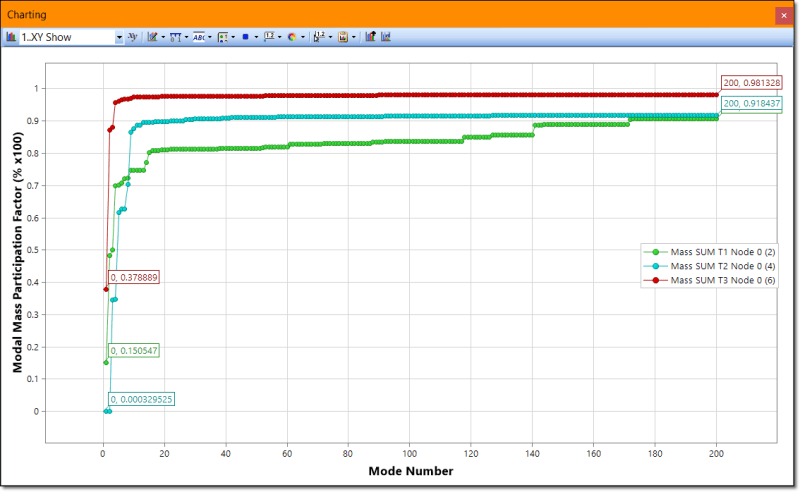
I have seen that in modal analyses, often there is a percentage for each mode which tells you how much of the overall mass is participating in that mode. I am using NASTRAN and have an output for the modal effective mass fraction but it is listed in each degree of freedom (x, y, z, rx...). See attachment
I am very confused as to how to combine these into a useful total effective mass fraction. Currently I have these 3 approaches:
1) Calculate the magnitude by doing sqrt(x^2 + y^2 ... +rz^2). This seems to be the most sensible, but does it make sense to do all degrees of freedom at once?
2) Simply sum all the values. I am sure this will give an answer that is too high, as mass that is rotating, can also be translating, so this mass would be double accounted for?
3) Select the highest value in any of the 6 degrees of freedom?. This feels wrong because changing the co ordinate system would give you the a different answer.
4) What I'm asking for doesn't exist Potentially the most likely. Why would NASTRAN not provide you with a total effective mass percentage for each mode, if it was a simple calculation? And why would I be struggling so much to find an answer.
Any help would be greatly appreciated!
Thanks
I have spent a couple of days fruitlessly searching forums for the answer, but I haven't found it yet so I thought I was ask it here.
I have seen that in modal analyses, often there is a percentage for each mode which tells you how much of the overall mass is participating in that mode. I am using NASTRAN and have an output for the modal effective mass fraction but it is listed in each degree of freedom (x, y, z, rx...). See attachment
I am very confused as to how to combine these into a useful total effective mass fraction. Currently I have these 3 approaches:
1) Calculate the magnitude by doing sqrt(x^2 + y^2 ... +rz^2). This seems to be the most sensible, but does it make sense to do all degrees of freedom at once?
2) Simply sum all the values. I am sure this will give an answer that is too high, as mass that is rotating, can also be translating, so this mass would be double accounted for?
3) Select the highest value in any of the 6 degrees of freedom?. This feels wrong because changing the co ordinate system would give you the a different answer.
4) What I'm asking for doesn't exist Potentially the most likely. Why would NASTRAN not provide you with a total effective mass percentage for each mode, if it was a simple calculation? And why would I be struggling so much to find an answer.
Any help would be greatly appreciated!
Thanks

![[smile] [smile] [smile]](/data/assets/smilies/smile.gif) .
.