Problem:
2 concentric holes that need to maintain a minimum distance between their walls.
If the larger hole, which provides the reference datum, is at its maximum tolerance the smaller hole can be more off its ideal position - see large view in below image.
Which would be the correct drawing call-out for the datum shift, the upper one with MMC for the datum or the lower one with LMC for the datum?
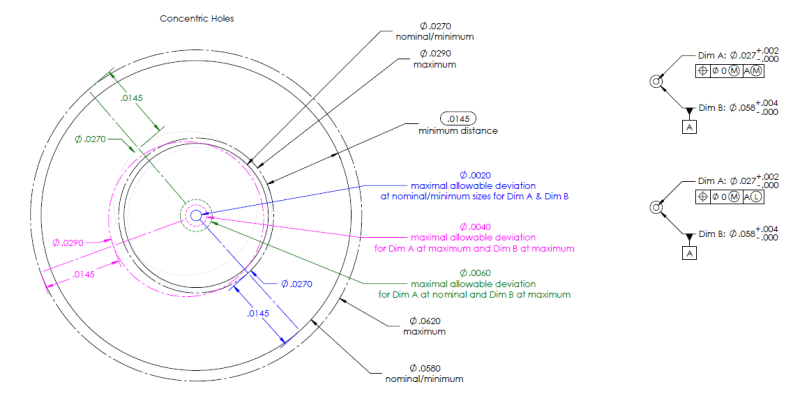
2 concentric holes that need to maintain a minimum distance between their walls.
If the larger hole, which provides the reference datum, is at its maximum tolerance the smaller hole can be more off its ideal position - see large view in below image.
Which would be the correct drawing call-out for the datum shift, the upper one with MMC for the datum or the lower one with LMC for the datum?

