Fascinating discussion. Among the products my company makes are carbon fiber composite tubes that fit within each other with 0.001" gap between them. The outer tube has an OD of 0.300" and a 0.025" wall thickness and 32" length, to give some perspective. Both the outer and inner tubes are designed to have similar bending stiffness so the inner tube has a greater wall thickness.
rb1957's intuition is correct. Without bonding there is no composite action.
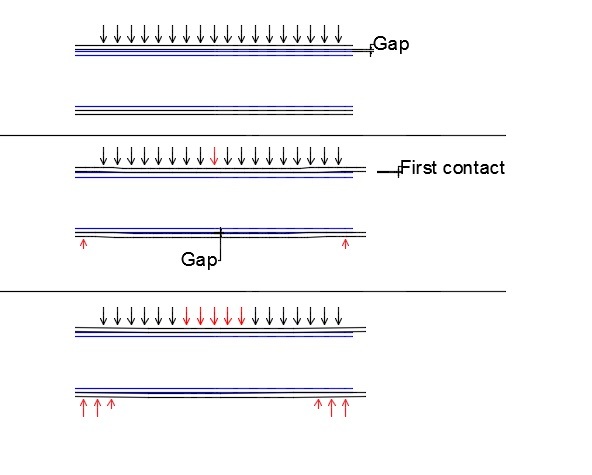
The logic that because the neutral axis is the same for both tubes whether they are bonded or not proves that there must be composite action is flawed. Let's take the case of three point bending. If you take the two tubes separately and bend them the same amount they will each have a certain load in the center of the span. If you place one tube in the other and deflect them the same amount, the measured load will be the sum of the loads measured for each tube. This is non-composite action. So why is this?
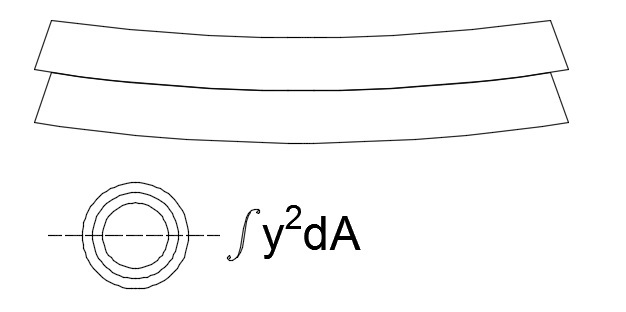
The factor that has been overlooked in all of the discussion so far, are the hoop stresses in the tube. When a tube is flexed it wants to ovalize where the tension and compression sides move closer together, which results in a lower "I" in axial bending. In an I-beam the web prevents this. In a tube only the walls can do this and they behave as two "C" shaped springs. So, with a tube in a tube that are not bonded you have four thin springs. When they are bonded they act as two thicker springs, which are stiffer than the four (composite action).
A unique feature of fiber reinforced composite material is that you can tailor material properties by changing the fiber orientations. One way to make a carbon fiber tube is by pultrusion, where fibers and resin are pulled through a shaping die. All the fibers are axial in the tube wall (think fiberglass tent poles). When flexed too far, these tubes fail by splitting axially because they ovalize, and there is no fiber reinforcement in the hoop direction. They have low axial stiffness because of the low hoop stiffness.
Tubes can also be made by table rolling where two sheets of unidirectional preimpregnated fibers (prepreg) are laminated together in a 0/90 orientation and then rolled around a steel mandrel and cured in an oven. Interestingly, a tube that is made from 50% 0 and 50% 90 fiber is stiffer in axial bending than a tube made from the same amount of fiber that is all in the 0 degree direction.