Cracking moment larger than moment of resistance? 1

[Woody1515]

Hello,

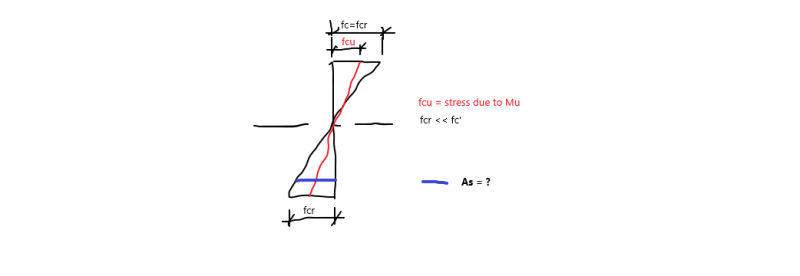
Is it possible for the cracking moment of a reinforced concrete beam to be larger than the ultimate moment of resistance? If I run the numbers with an 8” thick by 48” deep 30 MPa concrete beam with 2-15M bars top and bottom (very simple example) - I get a larger cracking moment than moment of resistance. This may be because the formula for the cracking moment has no resistance factors applied to it? Should I apply the 0.65 resistance factor to the cracking moment, since it is applied to the moment of resistance? I am trying to determine if the beam will crack under the factored ultimate loads.

This beam would be for a simple grade beam on piles supporting a new residential addition. The contractor wants to use a 48” deep beam as that is the only form he has available to him. The grade beam will be way stronger than what is required, but I want to know if the beam will even crack under the full design factored loads. Or in more general terms, can I compare the cracking moment (without a factor applied to it) to the factored loads?

 

[BridgeSmith]

AASHTO is imperial units (ksi). I forgot you guys were discussing metric equations. The equivalent to the 0.6 for f'c in MPa, is about .22 for f'c in ksi, so pretty close to the .24 constant in AASHTO.

AASHTO has dropped the 1.2 multiplier for Mcr, so it's just the minimum of Mcr or 1.33Mu (if Mu is smaller than Mcr, obviously).

Rod Smith, P.E., The artist formerly known as HotRod10

 

[Agent666]

Interestingly we still have the 1.33Mu limit, but only for load cases not involving lateral loads (wind or seismic). So to be honest this cuts out most building structures for obvious reasons.

We also have the 1.2Mcr limit, but only for PT design... Bit of a mixed bag!

In metric version of ACI318 I believe it's 0.62 instead of 0.6.

 

[rapt]

Agent666,

Unfortunately when the new NZS code decided to go its own way the geniuses who wrote it selected bits from different codes and unfortunately they got a few of the bad bits from some codes. The % reinforcement rules for RC are still sort of related to Mcr. They had to use 1.2Mcr for PT as it cannot be based on a %area simplification for bonded PT as it varies depending on the amount of PT.

AS code is 1.2Mcr as I said, but it is related to Mu, not phi Mu (for some silly reason no one can figure out) so it is effectively .85 * 1.2 Mcr so about Mcr, while Eurocodes is really 1.15Mcr!

 

[Settingsun]

Rapt, since there's hand-waving involved in justifying the use of the lower bound cracking stress instead of upper, what's another 15% one way or the other between friends?

 

[rapt]

Steveh49,

The ill-logic of not using phiMu doesn't worry me that much as discussed below. Just the fact of someone either accidentally leaving off the phi or or deliberately doing it without letting anyone know was a worry. When I pointed it out to several well respected members of the committee many years ago, they had not realized it was worded that way when AS3600 was created in 1988. And the section 9 slab rule was done based on phiMu rather than Mu because they did not realize this.

My preference would actually be a tension strain limit in the reinforcing. It is much more logical, especially in T-beams and in members using lower ductility reinforcement.

In a T-beam, The cracking moment rule puts more reinforcement in the negative moment region where the steel strain is smaller anyway, and less in the positive moment region where the steel strain is magnitudes larger. Completely the reverse to what a strain limit rule would do. If you want a member to be ductile and show a lot of deflection before collapse, you need to also limit steel strain as well as having sufficient reinforcement to carry the tension force on cracking.

And the cracking moment logic does not differentiate on steel ductility, where lower ductility steel requires lower strains so should require a higher minimum reinforcement requirement.

At least I was able to get this modified for steel fibre, if you look at the difference in the rules in AS5100 (which I am not involved in which allowed a lower minimum reinforcement and no strain limits) and AS3600 which removed the minimum reinforcement reduction, implemented strain limits and requires significantly higher minimum reinforcement for members requiring a fire rating or designed to resist earthquake actions (so just about all members).

 

[Settingsun]

I haven't thought strain limits through, but is imposing a lower limit on k_u equivalent? Both make intuitive sense to me: under-reinforcing is good to a point, but there can be too much of a good thing.

 

[mchen96]

You're not mentioning what is the applicable code for your project.

If you´re using ACI 318, the minimum reinforcement provision usually ensures that the section´s ultimate flexural capacity is greater than the cracking moment of the section. However, your situation (having a cracking moment greater than the ultimate flexural capacity) is allowed if the section's factored flexural capacity (not the cracking moment) is one third greater than the maximum factored load (see ACI 318-14 9.6.1.3).

AASHTO LRFD article 5.6.3.3 has a similar provision, in which the flexural capacity must be greater than (a) the cracking moment or (b) 1.33 times the factored load.

That being said, do consider the fact that any failure for a beam with a larger cracking moment than capacity will be brittle in nature.

 

[rapt]

steveh49,

A minimum ku limit is effectively a strain limit, assuming a fixed maximum compression face strain.

Michael,
If you read earlier posts, the 1.33 limit has been mentioned. Once they get rid of it from the code, the remainder of the minimum reinforcement rules in ACI and AASHTO will make a lot more sense! But this has developed into a general discussion on minimum reinforcement.

 

[r13]

I have a difficulty to grab the picture that brittle failure will occur, if a section is properly analyzed and designed for Mu, but with the situation that Mcr > Mu. Since Mu is a factored force estimated to be the maximum a member can experience, if under this maximum the concrete is intact (no flexural crack), that means the steel is not filly engaged, and the member can resist a load much higher than the factored load used in the design. After Mcr is reached, the steel start to carry more tension, note that at this stage the compression in the concrete is still relatively low, so failure would not occur. After crack, the mechanism is on path back to the ULS - the (minimum) steel has yield prior to crush of concrete, at a much much higher load level.

In the scenario above (Mcr > Mu), at force equal to Mcr, one needs to worry about shear rather than moment, as Vu was designed at the load level corresponding to Mu. Shall shear failure occurs prior to flexural failure, then name it a brittle failure mode is just.

 

[BridgeSmith]

As I understand the theoretical basis, with a very small reinforcing ratio, if cracks do develop, they are more likely to be few in number and large in width, leading to a higher probability of tensile fracture of the steel, rather than ductile yielding of the steel over a longer length.

Rod Smith, P.E., The artist formerly known as HotRod10

 

[JAE]

BridgeSmith is correct.

Also, it doesn’t matter what Mu is as the whole purpose of attempting to avoid brittle flexural failures is for cases where there is accidental overload and no ductile warning.

retired13’s comment about shear failing first in brittle fashion is a fair point except for the fact that sometimes shear capacity is designed for a much larger amount and also for the fact that shear capacity has a much larger variability than flexure (thus the smaller phi values) and can sometimes be way higher tha MN.

 

[r13]

Steel fracture is a build-in defect, if exists, the actual measurable As must be less than As[sub]min[/sub] considered in the design. For such condition, premature yielding can occur at any stress level (ie, M[sub]act[/sub]<Mu[sub]dgn[/sub]<M[sub]cr[/sub]), and the deflection will be large as the steel yield. The key is - when the steel yield with unusual large deflection, what is the stress in the compression zone, if it is much less than fc', can sudden failure occur? I think it could if the concrete can be sheared/teared through the crack as papers. Without defect in the steel (a necessary design assumption), the excessive load, beyond factored design load, required to produce the moment to fail the beam is already covered in my response above, and I think the possibility of w[sub]act[/sub] > w[sub]u[/sub] forms the base of prevention through strength reduction factors specified by the codes.

For shear concern, when Mcr > Mu, I suggest to have a close check on the shear strength at load leave that produces the Mcr, especially for beams classified as "deep" members.

 

[BridgeSmith]

Steel fracture is a build-in defect, if exists, the actual measurable As must be less than Asmin considered in the design.

While that is theoretically true, the 1.33 multiplier applied to the ultimate load is an additional factor of safety applied, in recognition that if the beam experiences a load much larger than the design loading, there is potential for a sudden catastrophic failure without warning. At the other end of the scale, overreinforced beams are typically avoided altogether for the same reason.

Rod Smith, P.E., The artist formerly known as HotRod10

 

[r13]

My argument is, besides shear concern, a beam reinforced with As[sub]req[/sub] will not fail in compression (brittle failure), as long as the actual load is within the code specified maximum, regardless other characteristic stress/force such as f[sub]cr[/sub], and Mcr. The 1.33 multiplier covers the possibility of overload (M[sub]act[/sub]>Mu[sub]dgn[/sub]), and the phi factor covers the uncertainty of the material. It is considered a balanced design when steel yield and the concrete crushes. If steel yield and concrete still has ample strength, it is a good design, because of the clear warning sign, deflection. An over reinforced beam is a design to be avoid, as the failure will likely be brittle, and sudden, without the benefit of deflection been noticeable.

 

[r13]

I think another way to look at this phenomenon, Mcr > Mu, is that the cross section must be very large, so the extreme tension side fiber has a stress resulting from Mu, fcu, that is less than fcr. From linear stress strain relationship, both fs and fc (compressive stress at compression side) are then less than fcr too. At this stage, the beam is essentially similar to a plain concrete element, which will not fail in flexural even without reinforcement. The beam will fail when fc > ∝fc', and fs > fy, both are on stress level much higher than fcr, IMO.

 

[Tomfh]

as long as the actual load is within

It might not be. That’s the whole point. Ductility provides a separate layer of safety by providing warning.

 

[r13]

Ultimate load = estimate real load * load factor, how large a load factor is required to get ride of the nightmare over load concerns?
I don't think you have read through the points.

 

[r13]

This is part of my reasoning, and question as well.

 

[rapt]

retired13

While most people think of brittle failure being an over reinforced phenomenon, You can also have a Brittle failure in an under-reinforced beam when the first crack occurs.

If the tension force required to create the first crack causes a strain in the tension steel greater than the failure strain, then the steel immediately snaps as the tension is transferred from the concrete to the reinforceemnt and you get a sudden collapse with little or no warning.

 

[r13]

If the tension force required to create the first crack causes a strain in the tension steel greater than the failure strain

Yes, agreed, if the stress is high enough, and sudden.

This is the key, and is the phenomenon that I've a difficulty to grab, as I couldn't find a similar case in my memory bank, though I'd dealt with thick structural elements for quite a long time. There were cases Mcr > Mu, but I'd never checked/calculated Mcr prior to finding As[sub]req[/sub] is less than code specified As[sub]min[/sub], and wanted to know the reason for sure. Shear had been always a concern though.