Datum features that aren't perpendicular 2

[elinah34]

Is there an option of defining 3 plsnar datum features that aren't perpendicular to each other as datums?
Sometimes there are cases in which the physocsl interfaces of the part aren't perpendicular, but still should be defined as datums since these are the functional interfaces and in addition fully constrain our part.
If it's ok, how is the coordinate system is defined in such cases? The coordinate system can't be Cartesian since the 3 datum features aren't perpendicular themselves.
If there is any reference for further reading it will be great.
Thanks!

 

[greenimi]

Datum features don't have to be perpendicular to each other.
Datums should be perpendicular to each other.

 

[elinah34]

Thanks, but how do you transform the not perpendicular set of datum features to perpendicular datums? How are the inspections reported? relative to the datums or to the datum features stimulators?
Is there any good example you can refer me to, so I will understand the entire process in such a case?

 

[greenimi]

Elinah34,

Are you working in ISO GPS or ASME?
If the latter then see figure 4-7 from ASME Y14.5-2009 (similar figure exist in 2018) "Inclined Datum Features"

 

[axym]

elinah34,

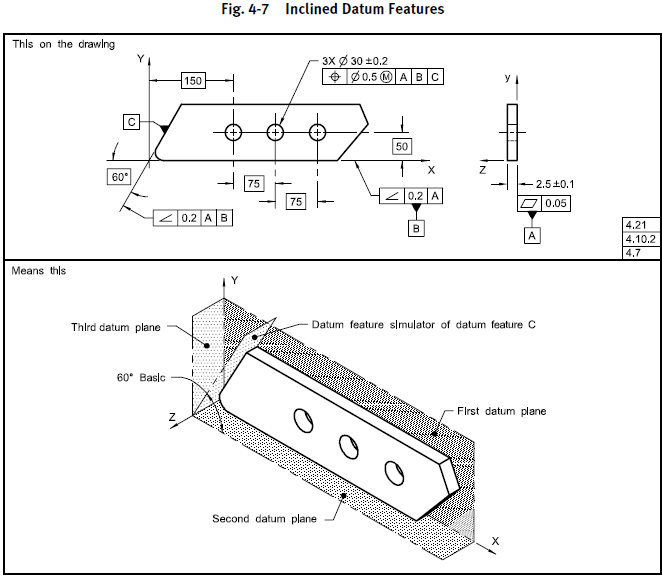
Further to what greenimi said, there can be 3 planar datum features that are not perpendicular to each other. Fig. 4-7 in 2009 (7-13 in 2018) is the only example in Y14.5 that illustrates this (that I can think of):

This figure shows that it is possible to specify planar non-orthogonal datum features and extract a Datum Reference Frame (Cartesian coordinate system). However, there are several misleading things in this example that have made it difficult to generalize to other cases (I have seen a lot of questions about this topic over the years).

The text in 7.10.2 states:

"For parts with inclined datum features as shown in Fig. 7-13, a true geometric counterpart plane is oriented at the basic angle of the datum feature. The corresponding plane of the datum reference frame passes through the vertex of the basic angle and is mutually perpendicular to the other two planes."

These statements are generally correct, but I would make the following comments:
-In this case with relatively simple part geometry, it is possible to make the plane of the datum reference frame pass through the vertex of the basic angle. In other cases, this will not be generally possible.
-This example also uses explicit datum reference frame identification (the drawing has explicit labels for the X, Y and Z axes). This technique is defined in Y14.5 and is a very good practice, but most drawings do not include these explicit labels.
-There is no particular procedure for defining a Cartesian coordinate system in three non-perpendicular planes. In other words, the origin and axis directions of the coordinate system are not uniquely defined if the explicit labels are not used.

Then there is the issue of the terminology that applies to the planes in the "means this" figure. This is where things get really confusing. The text in 7.10.2 uses the correct term "plane of the datum reference frame", but the figure uses the term "datum plane". Using these terms loosely has resulted in a lot of confusion - here's why:
-Each planar datum feature reference invokes a True Geometric Counterpart (TGC) that is a perfect plane at the basic angle of the datum feature
-A datum is extracted from each TGC. For planar datum features, the datum is a plane that is coincident with the TGC. So each planar datum feature reference invokes a datum plane that is at the basic angle of the datum feature.
-A Datum Reference Frame (three-plane Cartesian coordinate system) can be defined in the set of datums. Strictly speaking, these three planes are "planes of the datum reference frame" and not "datum planes".

Planar datum features, particularly when they are are orthogonal to each other, can be confusing because several of the different planes are coincident. So we have to be very fastidious with the terminology. Here are some comments on the planes shown in Fig. 7-13:

-The plane labeled "First datum plane" is:
1. The true geometric counterpart of primary datum feature A
2. Datum Plane A
3. One plane of the datum reference frame (the XY plane)

-The plane labeled "Second datum plane" is:
1. The true geometric counterpart of secondary datum feature B
2. Datum Plane B
3. One plane of the datum reference frame (the XZ plane)

-The plane labeled "True geometric counterpart of datum feature C" is:
1. The true geometric counterpart of tertiary datum feature C
2. Datum Plane C

The plane labeled "Third datum plane" is:
1. One plane of the datum reference frame (the YZ plane)

It is much easier to see the distinction between true geometric counterparts, datums, and planes of the datum reference frame in other examples that include datum features of size. Figure 7-5 is a good one - the datum features are a planar surface, cylindrical hole, and parallel-plane slot.

Evan Janeshewski

Axymetrix Quality Engineering Inc.

http://www.axymetrix.ca

 

[flash3780]

I think it's important to understand the difference between datum features and datums here.

The datum features are the features on the part used to immobilize the part in a Cartesian coordinate system.

The datum planes are the three planes of the coordinate system (X-Y ,Y-Z, X-Z). The origin of the coordinate system can be located anywhere in space relative to the datum features... whatever is convenient for the inspector.

When you specify datum references on a tolerance, you're telling the inspector how to hold the part while performing the inspection. E.g. Rest the part a face, then push it against a second face, and then against a third face.

Fig 4-7 above does a great job of showing the datum features (which are features on the part being inspected), the datum feature simulator (which is the physical thing that the part is immobilized on), and the X-Y-Z coordinate system (which can be thought of as a fixed-point/orientation on the datum feature simulator).

 

[Burunduk]

The datum planes are the three planes of the coordinate system (X-Y ,Y-Z, X-Z)

I prefer to differentiate between the concepts of the three perpendicular planes of the 'datum reference frame' (DRF) and the concept of datums - whether it is datum planes, datum axes, or datum points.

Datums are used as an auxiliary to construct the DRF. They are simulated by the 'datum feature simulators', and planar datums can be inclined relative to each other according to any basic angle and not just 90°. Just like a secondary datum axis, for example, doesn't have to be perpendicular to a primary datum plane, when a part feature has a specified tolerance that references a planar primary datum feature and a secondary datum feature hole/pin.

 

[flash3780]

I prefer to differentiate between the concepts of the three perpendicular planes of the 'datum reference frame' (DRF) and the concept of datums - whether it is datum planes, datum axes, or datum points.

I see what you mean, but I guess I have a hard time separating them. Really, the particular set of datum features specified in a FCF work together to establish a repeatable measurement coordinate system.

As shown in Fig 4-7, the actual datum planes are not necessarily in the same orientation as the features on the part. They are always three perpendicular planes. In a sense, the absolute orientation of the coordinate system (and datum planes) is unimportant. What we are establishing is the relative orientation and position of the coordinate system to features on the part.

If I specify a geometric tolerance, I typically need to locate the part within a Cartesian coordinate system (with 3 datum planes). In some cases, the orientation of the part in a particular degree of freedom within the coordinate system is irrelevant, so that degree of freedom is arbitrary and can be chosen by the inspector (e.g. a circular bolt pattern may not require any clocking control relative to other features on the part). In that case, the designer should only specify datum feature references which will immobilize the part in the degrees of freedom which are relevant to the function of the part.

The datum features referenced in the FCF instruct the inspector how to position and orient the part within a coordinate system. Different features on a part might be defined relative to different coordinate systems. The coordinate system (and the datums) are specific to a particular set of datum references in a feature control frame. If I change the datum features in a FCF, or even change the order of the datum feature references, I have to re-establish where my part is within a Cartesian coordinate system to perform that specific measurement.

You could even imagine that there is only one coordinate system in the world with 3 datum planes, and each set of datum feature references will place the part within that coordinate system at a known orientation and position.

 

[Burunduk]

As shown in Fig 4-7, the actual datum planes are not necessarily in the same orientation as the features on the part.

They sort of are. They are oriented per the basic dimensions between the features. 'Datum plane' C is simulated by "Datum feature simulator of datum feature C", and it is not the same plane as the "Third datum plane" - which is actually the third plane of the 'datum reference frame'.

I agree about how the datum references establish the coordinate system to position the part to, but 'datums' and DRF the planes (XY, YZ, XZ) are still separate concepts. A datum can be a plane, axis, line, point, and all sorts of combinations between them, and not even necessarily in an orthogonal structure.