jblc
Mechanical
- Apr 2, 2009
- 24
I'm unclear on why a motor model's step response isn't what i'd expect, when a damping coefficient (b) is varied.
With equivalent closed loop gains, I'd expect a shorter risetime for a motor with less damping...but instead, it looks like closed-loop step responses are identical to that of a higher damped system.
Say there's a DC motor with a Current I input, Angular Velocity θ_dot output. Optional Example: the "Load" block in [link mathworks.com/help/control/examples/dc-motor-control.html]Link[/url] (Ignore the Armature block).
Then θ_dot /I = Kt / (Js + b).
b is the damping coefficient, J the moment of inertia. Higher b means more damping, lower means less damping.
Prelim Question) In terms of step responses given a pole placement, write Kt / (Js + b) in time-constant form K / (Ts+1) :
(Kt/b) / [ (J/b)s + 1) ] --> T = J/b. Since T = 1/(-Pole), if T gets smaller as b grows larger, the Pole gets larger...so faster response?
Which doesn't make sense. Larger b should lead to a pole closer to the origin (since larger damping == slower response). Why is this not consistent?
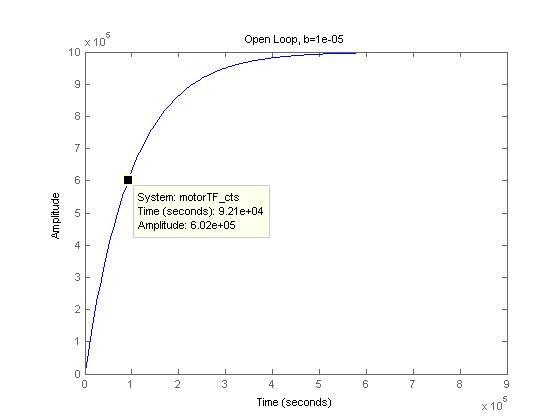
1) Now, regarding the identical closed-loop responses. Say b = 1e-5, Kt = 10, J = 1. Transfer Function TF =
10
---------
s + 1e-5
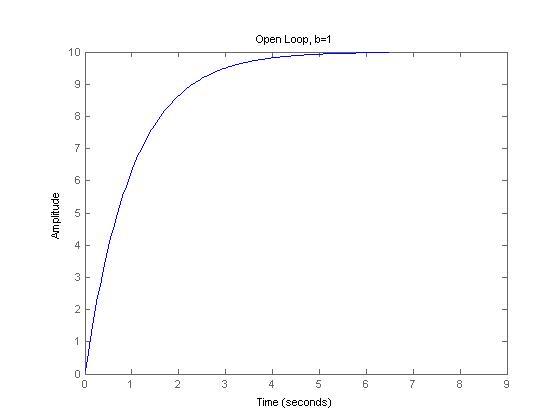
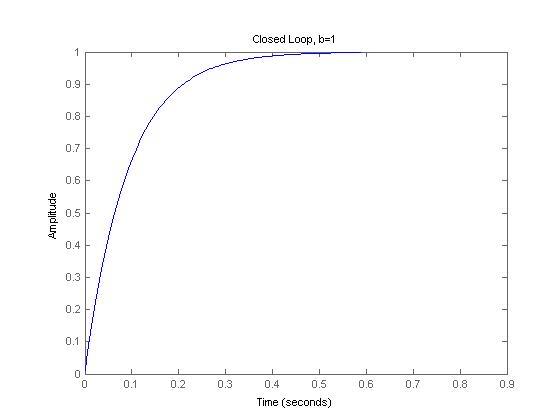
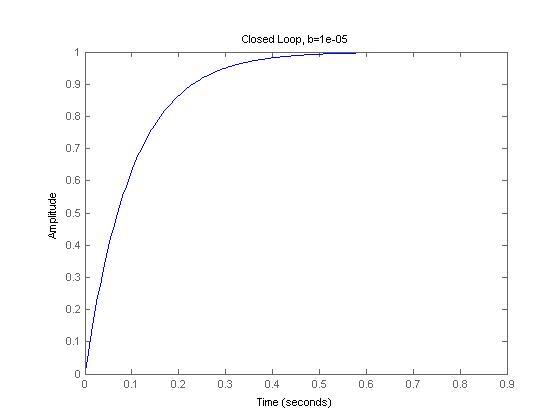
Open-loop and closed-loop step responses, with a simple closed-loop feedback gain of 1:
(See Matlab code at end of post if desired)
2) Say b decreases by a factor two (less damping) with b = 1/2 e-5. Transfer Function TF =
10
---------
s + 0.5e-5
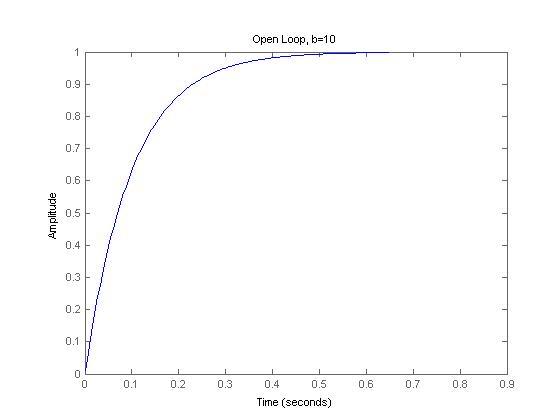
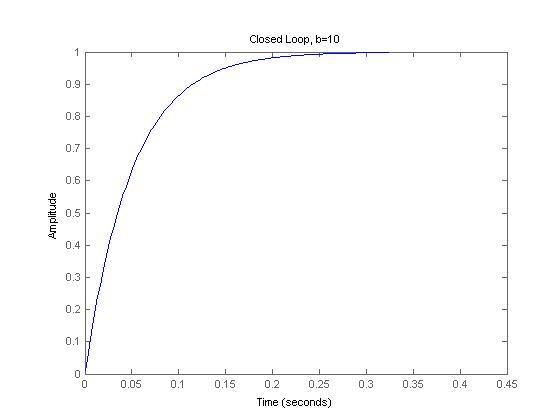
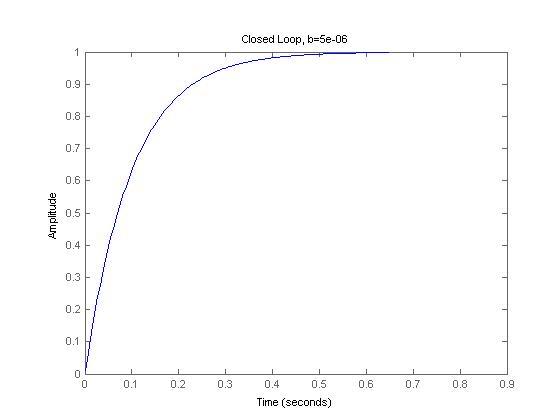
Open-loop and closed-loop step responses:
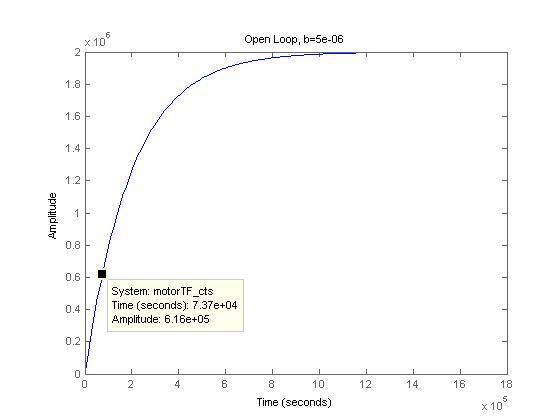
3) As expected, for open loop responses, the time to reach the same amplitudes (eg ~6e6) is indeed shorter for the lower damping case.
But the closed loop responses are identical.
Why isn't the risetime to 1 faster with lower b?
Code, just in case:
b = 1e-5; %or 0.5e-5
J = 1;
Kt = 10;
s = tf('s');
TF = Kt / (J*s + b);
step(TF);
title(['Open Loop, b=' num2str(b)]);
K = 1;
TF_FB = feedback(TF*K, 1);
figure;
step(TF_FB);
title(['Closed Loop, b=' num2str(b)]);
With equivalent closed loop gains, I'd expect a shorter risetime for a motor with less damping...but instead, it looks like closed-loop step responses are identical to that of a higher damped system.
Say there's a DC motor with a Current I input, Angular Velocity θ_dot output. Optional Example: the "Load" block in [link mathworks.com/help/control/examples/dc-motor-control.html]Link[/url] (Ignore the Armature block).
Then θ_dot /I = Kt / (Js + b).
b is the damping coefficient, J the moment of inertia. Higher b means more damping, lower means less damping.
Prelim Question) In terms of step responses given a pole placement, write Kt / (Js + b) in time-constant form K / (Ts+1) :
(Kt/b) / [ (J/b)s + 1) ] --> T = J/b. Since T = 1/(-Pole), if T gets smaller as b grows larger, the Pole gets larger...so faster response?
Which doesn't make sense. Larger b should lead to a pole closer to the origin (since larger damping == slower response). Why is this not consistent?
1) Now, regarding the identical closed-loop responses. Say b = 1e-5, Kt = 10, J = 1. Transfer Function TF =
10
---------
s + 1e-5
Open-loop and closed-loop step responses, with a simple closed-loop feedback gain of 1:
(See Matlab code at end of post if desired)


2) Say b decreases by a factor two (less damping) with b = 1/2 e-5. Transfer Function TF =
10
---------
s + 0.5e-5
Open-loop and closed-loop step responses:


3) As expected, for open loop responses, the time to reach the same amplitudes (eg ~6e6) is indeed shorter for the lower damping case.
But the closed loop responses are identical.
Why isn't the risetime to 1 faster with lower b?
Code, just in case:
b = 1e-5; %or 0.5e-5
J = 1;
Kt = 10;
s = tf('s');
TF = Kt / (J*s + b);
step(TF);
title(['Open Loop, b=' num2str(b)]);
K = 1;
TF_FB = feedback(TF*K, 1);
figure;
step(TF_FB);
title(['Closed Loop, b=' num2str(b)]);