Deflection Equations 2

[EngDM]

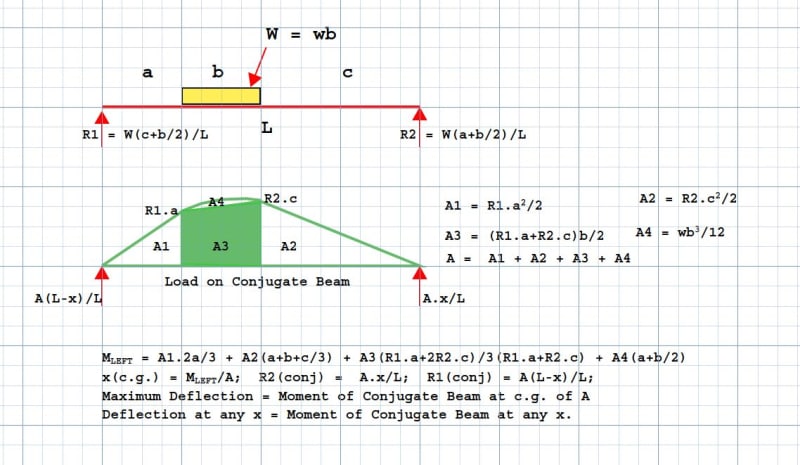
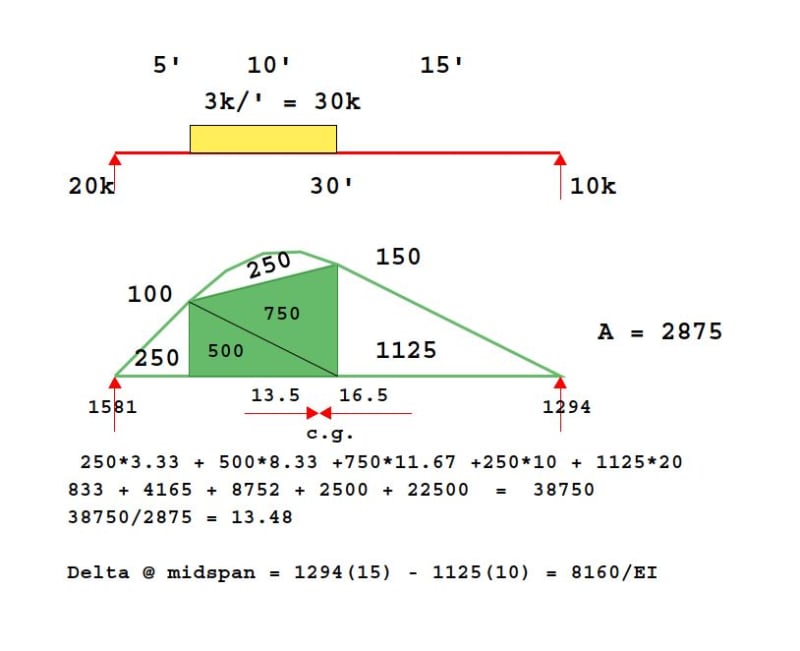
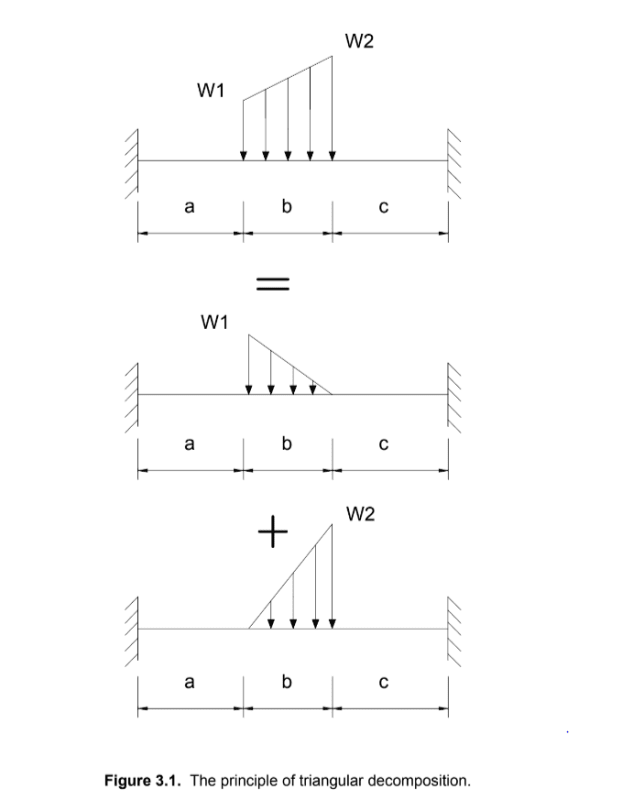
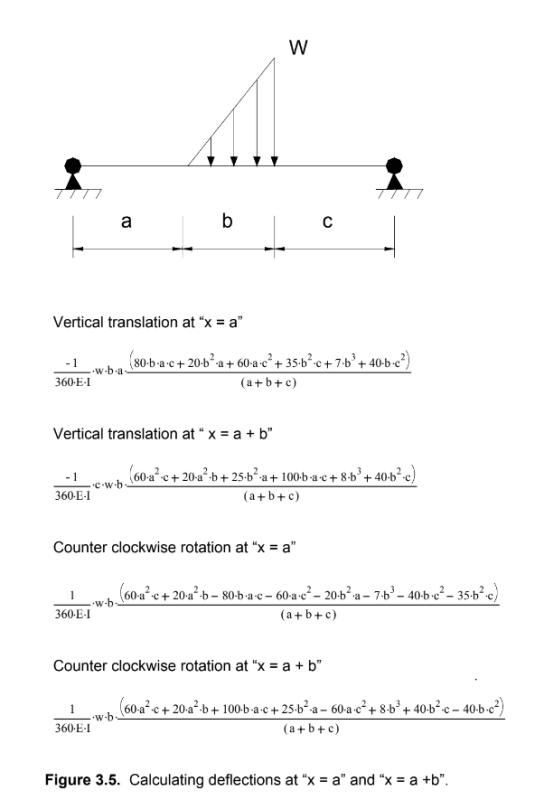
Hey all,

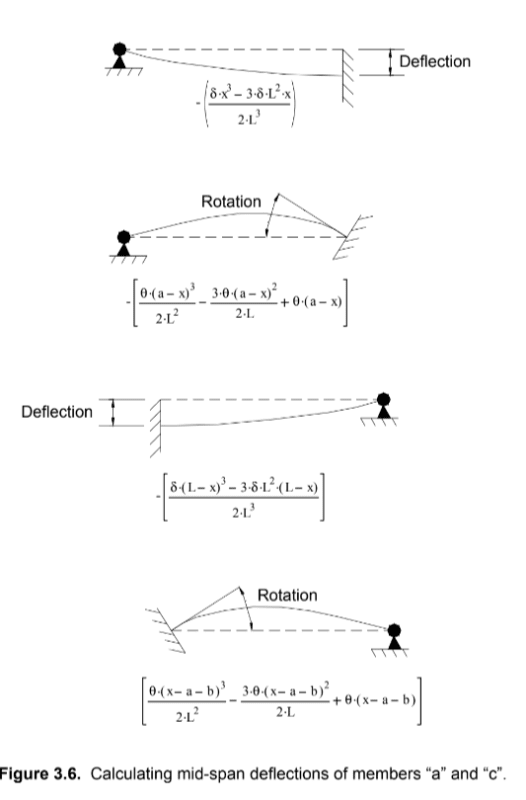
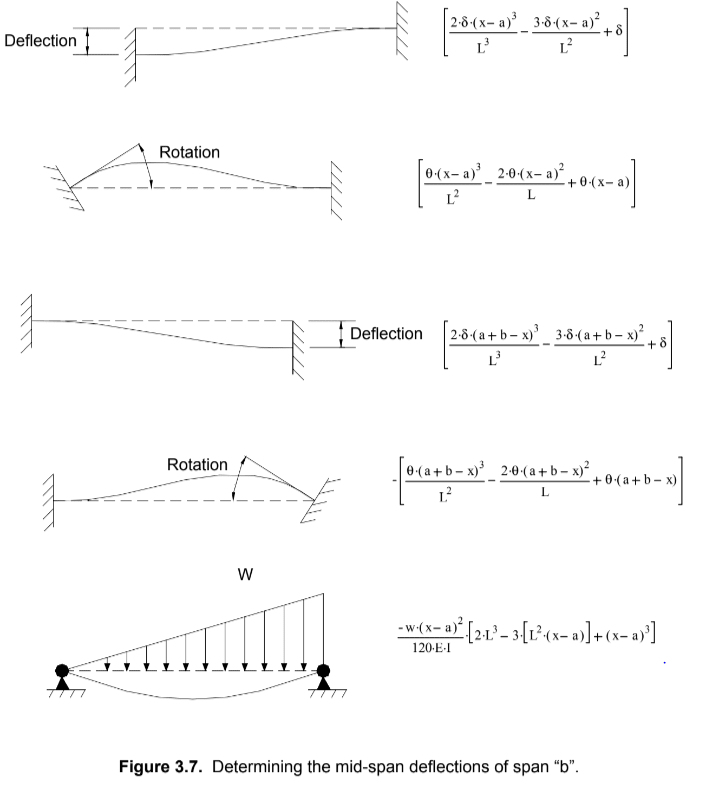
Anyone know of a resource to find a ton of different deflection equations? Everything I can find for a UDL not across the whole beam (and not located starting at a support) only gives the moment equation and no deflection.

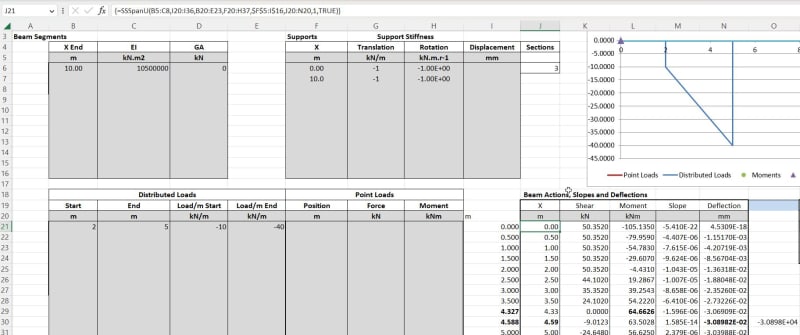
Or if you know of a good resource where they go over the derivation of the deflection equations. For weird cases I typically use clearcalcs or RISA 2D for quick results, but it would be nice to have a spreadsheet that uses the superimpose method.

 

[BAretired]

In most cases, finding deflection is an exercise to meet code requirements after having already selected a beam which has adequate strength. Often, the deflections are not a problem. When that is the case, there is no point in wasting design time performing useless work.

In the majority of cases, an engineer should be able to come up with a pretty good approximation with a minimum of effort.

An equal and opposite moment applied to each end of a beam results in a constant moment over the span. Slope and deflection of the real beam are equal to the imaginary shear Vc and bending moment Mc of the conjugate beam. The M/EI curve is the load imagined to be carried by the conjugate beam.

Bending moment for the conjugate beam is Wc*L/8, which is the deflection of the real beam loaded with constant moment across the span.
Wc*L/8 = M/EI*L[sup]2[/sup]/8 = M/EI*L[sup]2[/sup]/8 = WL/8EI*L^2/8 = wL[sup]4[/sup]/64EI.

With a little practice, an engineer should be able to estimate deflections quite accurately. In those rare cases where it is necessary, one must sharpen the pencil a bit.

 

[dvd]

Blodgett books have several beams with deflections

Design of Welded Structures

Design of Weldments

 

[BAretired]

Structural engineers should get a feel for the magnitude of deflection to be expected. Study the shape of the bending moment curve and estimate the deflection, even if it turns out to be a waste of time to perform a detailed calculation.

 

[centondollar]

Structural engineers should get a feel for the magnitude of deflection to be expected. Study the shape of the bending moment curve and estimate the deflection, even if it turns out to be a waste of time to perform a detailed calculation.

Estimating the shape of bending moment and deflection curves is not the same as estimating their magnitude. Without calculations (and they will be complicated and long if done by hand for non-trivial cases seldom found in table books such as variable-span or variable-stiffness continuous beams with non-uniform load), the procedure of checking magnitudes is not possible.

EDIT: Of course one can apply the unit load theorem and compute deflection or rotation at discrete points by using the bending diagram, but that also requires a lot of algebra (or alternatively Excel) for any non-trivial structure.

 

[Stress_Eng]

Just to introduce a side-line to the subject, the tools at hand to the engineer can start with the traditional book reference for the classic hand calc, such as Roark. As the problem gets more difficult, other tools start to come in handy, such as Excel. One tool that I have found to be very useful for the case where the problem is more complex, involving aspects such as end restraints, point forces / supports, step moments and / or different shapes of distributed loading and changing cross section, Mathcad has proven to be very useful. Bending moment, section inertia and integral functions can be set up with unknown variables included. The necessary number of equations to solve for the unknowns can be constructed. This obviously is based on first principals(prismatic and non-prismatic). The top of the list would probably be FEA.

 

[BAretired]

Anyone know of a resource to find a ton of different deflection equations? Everything I can find for a UDL not across the whole beam (and not located starting at a support) only gives the moment equation and no deflection.

Or if you know of a good resource where they go over the derivation of the deflection equations. For weird cases I typically use clearcalcs or RISA 2D for quick results, but it would be nice to have a spreadsheet that uses the superimpose method.

Here is a case of a partial uniform load on a beam. It would be good for a spread sheet I think, and you could use a separate line for each different kind of load. Two or three lines should be enough for most beams, but there is no limit. In the end, the spread sheet would sum the values at each station, showing a composite deflection diagram.

 

[BAretired]

I substituted some values and my results are shown below. Have not checked to see if they are reasonable. Will do so in due course.

 

[BAretired]

For a 30' span with a point load of 30k centred 10' from one end, the moment would be Pab/L = 30*10*20/30 = 200'k. Deflection at point of load would be Pa[sup]2[/sup]b[sup]2[/sup]/3EIl, or 30*(10*20)[sup]2[/sup]/3EI*30= 13,333/EI, considerably more than my result 8160/EI but looks believable.

The method needs more testing, but the OP should be optimistic about using a spreadsheet.

 

[KootK]

1) I believe that I solved this problem back in 1999 in the course of developing some software. The key to my method is to recognize that any possible uniformly varying load can be treated as the superposition of two triangular loads. For the triangular cases, I used shape functions and integration to get the job done (with MathCAD's help).

2) I would not blame you for doubting the accuracy of these equations. That said, I vetted the crap out of them and actually found bug in S-Frame in the process of doing so. I've also been using these equations for about 20 years in some MathCAD design sheets without incident.

3) Realistically, the hardest part of getting this right is typing out the equations properly.

4) The closed form solutions run wicked fast in MathCAD relative to iterative or discretized approaches which is helpful there.

 

[oengineer]

This link contain deflection equations that are not in the steel manual:

https://awc.org/wp-content/uploads/2021/12/AWC-DA6-BeamFormulas-0710.pdf

 

[BAretired]

Very nice, KootK. There really are a number of ways of solving the problem, but during the course of designing a building, I rarely checked it by calculation because there were usually enough comparisons or obvious clues indicating that the member was code compliant without going through all the work. One method which I used occasionally was Newmarks Numerical Procedures. Even had it included in SlideRuleEra's files...but not any more.

 

[BAretired]

This link contain deflection equations that are not in the steel manual:

https://awc.org/wp-content/uploads/2021/12/AWC-DA6...

Yes thank you, it's quite a good table, but in some cases, deflections are not displayed.

 

[rb1957]

yes, many ways to skin cats, and very neat manipulation, but the deflection at the mid-span is not the maximum (though near enough for practical purposes).

I agree with BA, that this is typically not critical for design (so this may be wasted effort).
but I think we should learn things for ourselves (rather than to rely on what we read on the "interwebs").

I would (and have) solved the deflection of the beam mathematically in excel. Solve a couple of simple loadings and you can solve any load and determine the maximum deflection. And with a little more effort different end conditions.

And try things, like compare a full span UDL with a point load, compare a mid-span point load with a point load at "x".

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[Stress_Eng]

I do like the idea of creating a library of different beam loading conditions, and the obvious first place to look is the readily available hand calc text books and manuals. At some point those places of information will run dry when the problem gets complicated. That’s when you are going to have to choose the right tool for the job, be it Excel, Mathcad or some other (Matlab, Maxima, endless list) and go back to first principals and create the equations yourself. That’s when the fun begins! At some point you may hit the limits of your trusted tool and have to find one more capable. To meet the increasing complexity of your beam analysis cases, you may end up with a library of templates based on various tools.

 

[Stress_Eng]

Attached is just an example of an alternative approach to carrying out a beam analysis. The method applied hasn't been checked or validated.

 

[IDS]

The method applied hasn't been checked or validated.

I ran it in my ConBeamU spreadsheet (using the single span function) and got exactly the same results (to displayed precision).

Using the spreadsheet, if it is important to get the position of maximum deflection and/or bending moment the Excel solver does a good job of finding that. For the deflections I multiplied the deflection by 1E6 in the adjacent column, to save adjusting the solver tolerance, or I could have just set the deflection units to nanometres.

I also checked baretired's example and got significantly different results, but I will double-check the units on that one before posting the results.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Stress_Eng]

Thanks for the feedback IDS, nice to know your results were the same.

 

[skeletron]

Loving the discussion and ways to skin the proverbial cat. If push comes to shove, and if this was in a production environment, I would just run a check in a 2D Frame analysis program versus trying to create a beam sheet that can handle lots (if not all) loading conditions. Or, potentially run SymPy and run with it...YMMV

 

[BAretired]

I also checked baretired's example and got significantly different results...

...gulp!

 

[IDS]

I just checked the Stress-eng example in my FEA software with the beam divided into 10 segments. The magnitude and location of the maximum bending moment agreed exactly, and this is reported in the standard output. The location of the maximum deflection was reported as 4.60 m (compared with 4.588 m) and the magnitude only agreed to 5 significant figures

Deflections are found by fitting a cubic shape function to the deflections calculated at beam ends, so it is not surprising that there are small differences compared with our calculations, where we adjusted the beam end locations to find the "exact" maximum deflections.

Note that all these calculations are ignoring shear deflections, which would have a far bigger effect than the 6th significant figure.

BA - I'll post my results later. They were the same order of magnitude as yours


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/