jjalex1
Structural
- Jan 3, 2012
- 22
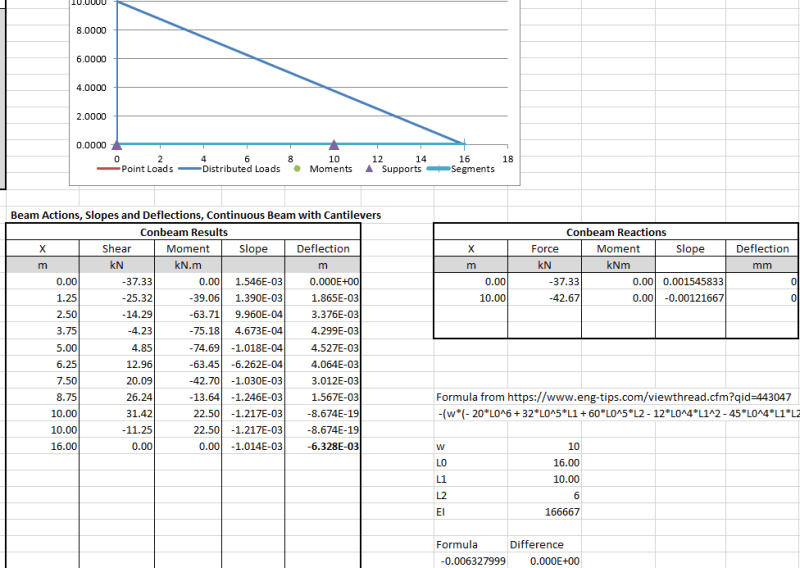
Does anyone know what's the deflection formula for a beam overhang one support for a triangular distributed load over the entire beam? Beam is supported by two supports.
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
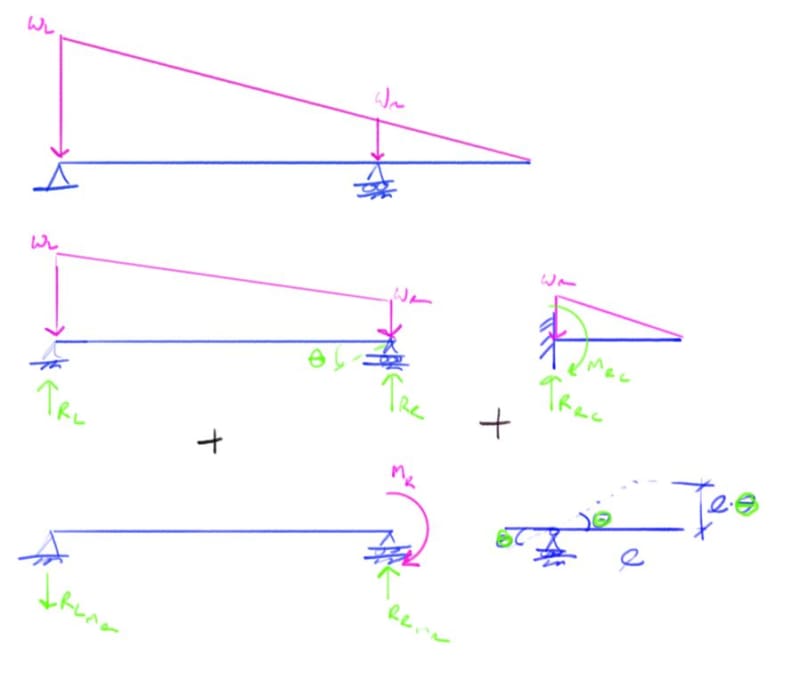
Delta = -(w*(- 20*L^6 + 32*L^5*L1 + 60*L^5*L2 - 12*L^4*L1^2 - 45*L^4*L1*L2 - 60*L^4*L2^2 + 20*L^3*L2^3 + 10*L^2*L1*L2^3 + 3*L1*L2^5))/(360*EI*L1^2)
…
Please check to make sure you agree before using it.