BILL486
Mechanical
- Mar 30, 2004
- 2
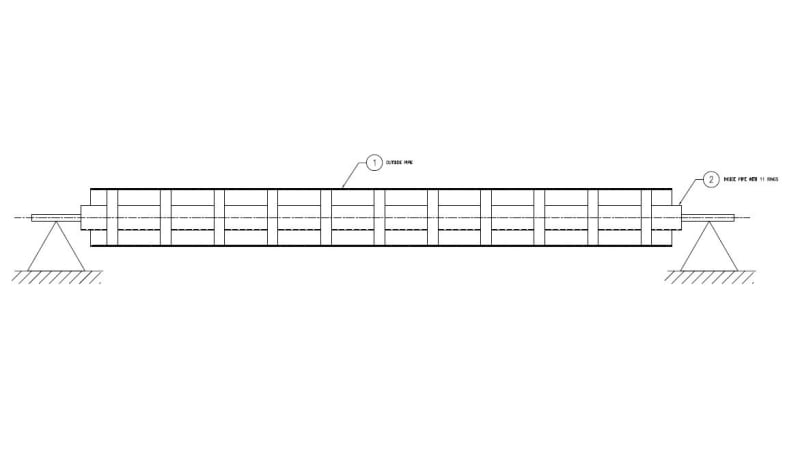
I have to find out deflection in a 12" pipe with fixed bearing supports at both ends. However, the ID of this pipe has an internal smaller pipe with equally spaced 1" wide rings (donuts) plug welded in place for better support internally. My question is, how do I calculate deflection of the entire assy? Would I have to neglect the welds?
Thanks,
Bill H.
Thanks,
Bill H.

![[idea] [idea] [idea]](/data/assets/smilies/idea.gif)