Deflection Of A Mass Due To Centrifugal Force

[Daparojo252]

I am trying calculate the theoretical displacement of a mass that is fixed at one end, the other rigid due to a centrifugal force acting on a mass.
Where the other end is rigid, it subject to a tightening load against the application face, hence the centrifugal force, F has to overcome the force acting on the Nut due to tightening and friction to create the displacement. FF0.15.

Please see the file, and please comment if I can improve on this.






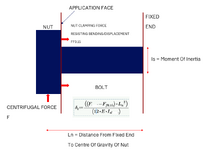
Thanks in advance.

 

[Stress_Eng]

Don't know if this is of any help. It hasn't been checked and it was to do with a different post some time back, but it may give you some ideas.

 

[IRstuff]

Per your drawing, the clamping force only affects displacement forces in the axial direction of the fastener. Your F would tend to cause displacement perpendicular to that axis, so that's resisted mostly by friction, isn't it?

 

[Stress_Eng]

If friction is not overcome, then you can effectively assume the mating surfaces of the nut and clamped material are bonded (or fused). Then the force traversing the interface will enter the clamped material, causing a diminishing shear displacement through the thickness and (increasing shear area with depth) and a linearly increasing bending moment (I increases with depth). You could assume the force propagates into a cone shaped material, at an angle of 45 degrees. That angle could differ. An angle to use could be the same as that used to encompassing the clamped material when calculating the compression stiffness used in preloading calculations. You will have two load paths acting in parallel (same shear displacement and rotation due to bending), the clamped cone and the bolt (assuming different materials, i.e. E and G).

If friction is overcome, then you'll have a state of sliding friction. A number of stress conditions will be introduced. The bolt head will slide, putting the bolt shaft into bending (assume S shape), shear and tension, whilst, at the same time, the clamped material will see compression and shear due to sliding friction. This is assuming no bolt head rotation and there's clearance between the bolt and the hole. A state of equilibrium will occur, where the work done by the displaced force equates to the introduced internal strain energy. Don't forget, the friction will aid you!

Sounds like an interesting problem!

 

[IRstuff]

Sounds like an interesting problem!

Possibly, but as stated in the OP, a constant force isn't likely to do much, since it has to have a shear component to do anything; otherwise, the surface, through friction, will simply carry the nut along for the ride. Only through mismatched phase, i.e., nut going north, while substrate goes south, is there likely to be anything interesting happening.