Logan82
Structural
- May 5, 2021
- 212
Hi,
What would be the equation of the deflection of the two beams stacked stacked on each other? I am looking for the deflection at a distance "a" from the support.
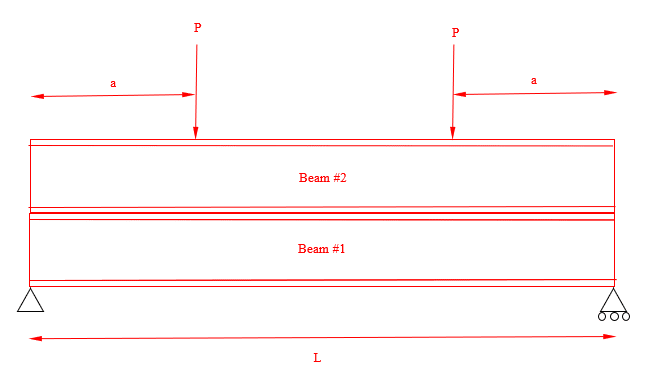
Assumptions:
- The two beams are not linked to another, they are just stacked.
- We can assume that there is no friction.
- The two loads are symmetrical.
- The two beam shapes are different.
I know that:
- The deflections are equal (Δ1 = Δ2).
- The equation of the deflection if there was one beam would be:
Δx = (P*x*(3*L*a-3*a^2-x^2))/(6*E*I)
Since we are looking for the deflection at x = a, then:
Δa = (P*a*(3*L*a-4*a^2))/(6*E*I)

What would be the equation of the deflection of the two beams stacked stacked on each other? I am looking for the deflection at a distance "a" from the support.

Assumptions:
- The two beams are not linked to another, they are just stacked.
- We can assume that there is no friction.
- The two loads are symmetrical.
- The two beam shapes are different.
I know that:
- The deflections are equal (Δ1 = Δ2).
- The equation of the deflection if there was one beam would be:
Δx = (P*x*(3*L*a-3*a^2-x^2))/(6*E*I)
Since we are looking for the deflection at x = a, then:
Δa = (P*a*(3*L*a-4*a^2))/(6*E*I)

