Eng-Tips is the largest engineering community on the Internet
Intelligent Work Forums for Engineering Professionals
Design of shear studs connected to soldier pile walls/concrete facing 1
- Thread starter t230917
- Start date
- Thread starter
- #21
Yes, there is only 1 drilled shaft that encases the soldier pile and supports the facing as well.
Thank you @retired13for the details as well. They will help.
To get back to the shear studs, I understand that it is a continuous concrete deck on steel beams with linearly varying loads. I have designed the concrete facing. Should the next step be to get the shear on the supports (soldier piles), i.e. V and multiply it with the transformed/composite properties "Q" and divide by the composite moment of inertia to get the shear flow?
Thank you @retired13for the details as well. They will help.
To get back to the shear studs, I understand that it is a continuous concrete deck on steel beams with linearly varying loads. I have designed the concrete facing. Should the next step be to get the shear on the supports (soldier piles), i.e. V and multiply it with the transformed/composite properties "Q" and divide by the composite moment of inertia to get the shear flow?
- Thread starter
- #23
So, I found the shear flow. I multiplied it by 12" to get the shear per foot of the wall. I calculated Qr=phisc*Qn to get the strength of the shear studs.
Is this it? How do I get the max. and min. pitch?
For a 12" section of the wall, I am getting a shear of 8.21 kips, and the strength of the individual shear studs as 21.04 kips. Is that reasonable?
Is this it? How do I get the max. and min. pitch?
For a 12" section of the wall, I am getting a shear of 8.21 kips, and the strength of the individual shear studs as 21.04 kips. Is that reasonable?
What equation you were using to calculate the shear flow? It is simpler to use f = VQ/I (ignore b at the denominator), so the result is force per inch in direction of the longitudinal axis (kips/in/width). Then, s = capacity (kips)/shear flow (kips/in). In your case, assume the calculation is correct, s = 21.04/8.21 = 2.56" - too close, try larger stud with 2 in a row to getting better result.
- Thread starter
- #25
-
1
- #26
The thing that draw my attention is the statement - "I multiplied it by 12" to get the shear per foot of the wall. Let's think about, if the demand is only 8.21 kips within one foot distance, then 21.04 capacity is way beyond the demand, correct? In such a case, you shall reduce the capacity (select a smaller stud) to get into a more reasonable spacing.
Let's start from the beginning, what is the spacing of the steel beam? Your V shall equal to the reaction at the base, 8 kips seems too small. For example, a wall 10' height with 40 psf lateral load, and a tributary width of 10', R = 0.04*!10^2/2)*10 = 20 kips at the base, then V = 20 kips, which is to be used for stud design Please double check your load.
Let's start from the beginning, what is the spacing of the steel beam? Your V shall equal to the reaction at the base, 8 kips seems too small. For example, a wall 10' height with 40 psf lateral load, and a tributary width of 10', R = 0.04*!10^2/2)*10 = 20 kips at the base, then V = 20 kips, which is to be used for stud design Please double check your load.
- Thread starter
- #27
Ok, starting form the beginning. Wall is 13.25 feet, ka=0.47, gamma = 0.12 kcf, distance between soldier piles = 12 feet.
Earth pressure = ka*gamma*H=0.75 ksf/ft. Live load surcharge = 250psf*ka = 0.12 ksf/ft.
Max. shear = 1.1*wl = 1.1*12*(1.5*0.75+1.75*0.12) = 17.5 kips (I am using reaction as 1.1wl for continuous spans)
Shear flow = VQ/I = 17.5*209/5359 = 0.68 kips/in
For 12" - Shear = 8.21 kips
Qr = 21.04 kips.
Am I making a mistake in the loading?
Earth pressure = ka*gamma*H=0.75 ksf/ft. Live load surcharge = 250psf*ka = 0.12 ksf/ft.
Max. shear = 1.1*wl = 1.1*12*(1.5*0.75+1.75*0.12) = 17.5 kips (I am using reaction as 1.1wl for continuous spans)
Shear flow = VQ/I = 17.5*209/5359 = 0.68 kips/in
For 12" - Shear = 8.21 kips
Qr = 21.04 kips.
Am I making a mistake in the loading?
- Thread starter
- #28
For per foot of soil behind the wall:
Surcharge pressure = 0.25*0.47 = 0.1175 klf/ft
Soil pressure at bottom = 0.12*13.25*0.47 = 0.7473 klf/ft
Force due to surcharge = 0.1175*13.25 = 1.56 k/ft
Force due to soil = 0.7473*13.25/2 = 4.95 k/ft
Total force at bottom of the cantilever beam = 1.56+4.95 = 6.51 k/ft
For 12' beam spacing, with 1.1 multiplier:
R = 6.51*12*1.1 = 85.9 kips, say 86 kips
Shear flow f = 86*209/5359 = 3.35 k/in
For Qr = 21.04 kips, spacing of studs, s = 21.04/3.35 = 6.28" ---> use 1 stud @12", or 2 studs @ 12".
Surcharge pressure = 0.25*0.47 = 0.1175 klf/ft
Soil pressure at bottom = 0.12*13.25*0.47 = 0.7473 klf/ft
Force due to surcharge = 0.1175*13.25 = 1.56 k/ft
Force due to soil = 0.7473*13.25/2 = 4.95 k/ft
Total force at bottom of the cantilever beam = 1.56+4.95 = 6.51 k/ft
For 12' beam spacing, with 1.1 multiplier:
R = 6.51*12*1.1 = 85.9 kips, say 86 kips
Shear flow f = 86*209/5359 = 3.35 k/in
For Qr = 21.04 kips, spacing of studs, s = 21.04/3.35 = 6.28" ---> use 1 stud @12", or 2 studs @ 12".
- Thread starter
- #30
Per the calculation, you can use 1 stud @3" from the bottom, then place the studs every 6" until the space can be lengthened (the shear force diminishes upward).
One important force to be included in your calculation - tension, due to soil pressure pushes the wall away from the support beam. The stud capacity will be reduced for the combined effects.
One important force to be included in your calculation - tension, due to soil pressure pushes the wall away from the support beam. The stud capacity will be reduced for the combined effects.
- Thread starter
- #34
So, does the tension in the unit load strip = 0.1175 klf/ft+0.7473 klf.ft = 0.86 klf/ft; and we multiply this with the span length of 12 feet to get t=0.86*12 = 10.38 k/ft?
Does the total Qr then get reduced from 21.04 kips to 21.04-10.38 = 10.66 kips?
Does the total Qr then get reduced from 21.04 kips to 21.04-10.38 = 10.66 kips?
- Thread starter
- #35
Another related question: Do we need to consider the weight of the concrete panel as a load that needs to be resisted by the shear studs?
Also, I have taken the Q and I as composite properties: do these need to be only the pile properties since we are not looking for composite action?
Also, I have taken the Q and I as composite properties: do these need to be only the pile properties since we are not looking for composite action?
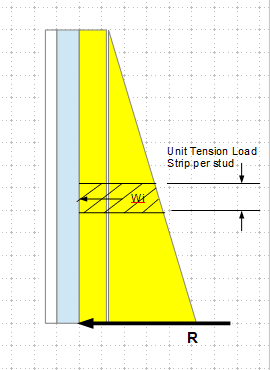
The calculation of tension is treating the wall panel as horizontal beam supported by the steel beams, and find the reaction. For example, for 1' strip from the bottom:
p[sub]13.25[/sub] = 0.7473+0.1175 = 0.8648
p[sub]12.25[/sub] = 0.6909+0.1175 = 0.8084
Wi = (0.8648+0.8084)/2 = 0.8066 ((note, intensity of Wi reduces from bottom up)
t = 0.8066*12 = 9.68 kips
With the obtained f & t, go to AISC J3.7 to determine the anchor strength for combined tension and shear in bearing type connection.
For your latter question, yes, the panel weight needs to be considered. I suggest to have continuous footing under the panel to transfer the weight directly into ground, to reduce the chance that over load the steel beams. Otherwise, you have to add the weight to the shear flow for connector design.
Yes, without design as a composite, your wall panel wouldn't be stand still. A floor slab can be designed either as composite, or non-composite; however, flip the slab-beam upside down in hanging ceiling-like manner, then the only choice will be composite. When in doubt, just ask "is the connection between the panel and the beam is necessary for the system to function properly?" Hope this helps.
p[sub]13.25[/sub] = 0.7473+0.1175 = 0.8648
p[sub]12.25[/sub] = 0.6909+0.1175 = 0.8084
Wi = (0.8648+0.8084)/2 = 0.8066 ((note, intensity of Wi reduces from bottom up)
t = 0.8066*12 = 9.68 kips
With the obtained f & t, go to AISC J3.7 to determine the anchor strength for combined tension and shear in bearing type connection.
For your latter question, yes, the panel weight needs to be considered. I suggest to have continuous footing under the panel to transfer the weight directly into ground, to reduce the chance that over load the steel beams. Otherwise, you have to add the weight to the shear flow for connector design.
Yes, without design as a composite, your wall panel wouldn't be stand still. A floor slab can be designed either as composite, or non-composite; however, flip the slab-beam upside down in hanging ceiling-like manner, then the only choice will be composite. When in doubt, just ask "is the connection between the panel and the beam is necessary for the system to function properly?" Hope this helps.
- Thread starter
- #37
- Status
