NewbieInSE
Structural
- Dec 19, 2019
- 234
Hello Engineers,
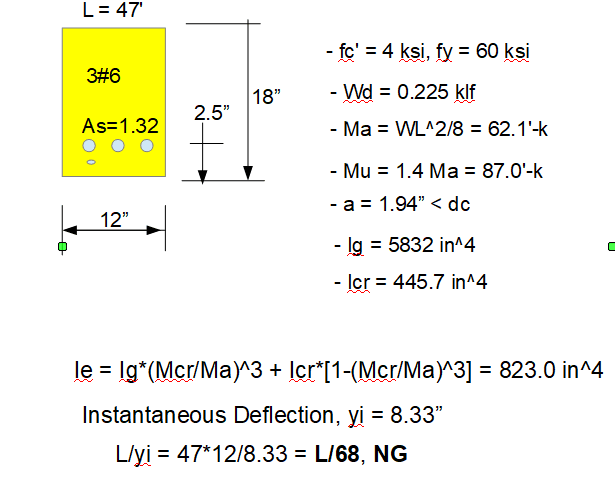
I'll elaborate it. Say i have a concrete beam having some dimensions, its moment capacity for singly reinforced criteria is 400 kips-ft, say. Moment induced from loads in that beam at the certain location is say 330 kips-ft. It means i can design it as singly reinforced, and say reinforcement requirement is 2.5 in^2 as singly reinforced section.
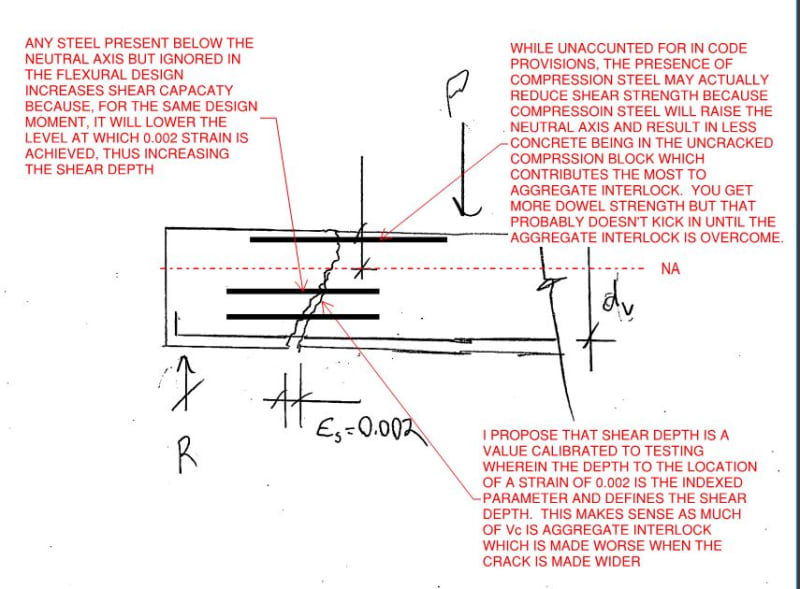
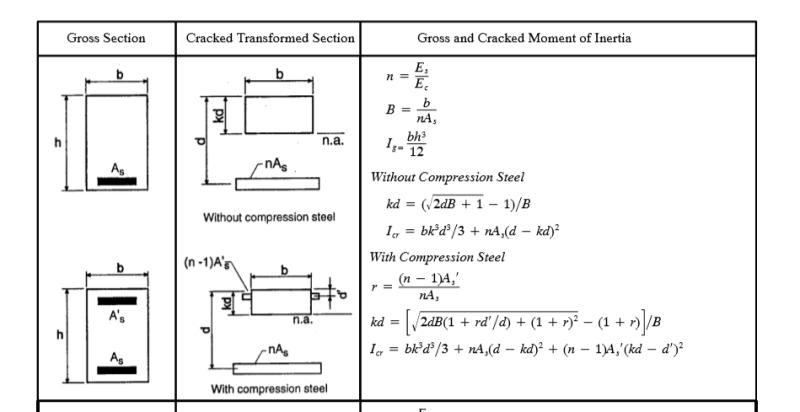
My question is can i design that section of 330 kip-ft moment requirement, as a doubly reinforced section requiring bottom reinf. say 2.3 in^2, and at top say from calculation .6 in^2 or anything. I think it is possible, considering bottom reinforcement is yielding, but want to know in depth.
I'm actually asking it for existing structural members, which contain less reinforcement (bottom) than required when considered singly reinforced, but contain some top reinforcement which maybe could help in forming doubly action.
Thanks.
I'll elaborate it. Say i have a concrete beam having some dimensions, its moment capacity for singly reinforced criteria is 400 kips-ft, say. Moment induced from loads in that beam at the certain location is say 330 kips-ft. It means i can design it as singly reinforced, and say reinforcement requirement is 2.5 in^2 as singly reinforced section.
My question is can i design that section of 330 kip-ft moment requirement, as a doubly reinforced section requiring bottom reinf. say 2.3 in^2, and at top say from calculation .6 in^2 or anything. I think it is possible, considering bottom reinforcement is yielding, but want to know in depth.
I'm actually asking it for existing structural members, which contain less reinforcement (bottom) than required when considered singly reinforced, but contain some top reinforcement which maybe could help in forming doubly action.
Thanks.