m.piron
Mechanical
- Sep 20, 2019
- 16
Good morning.
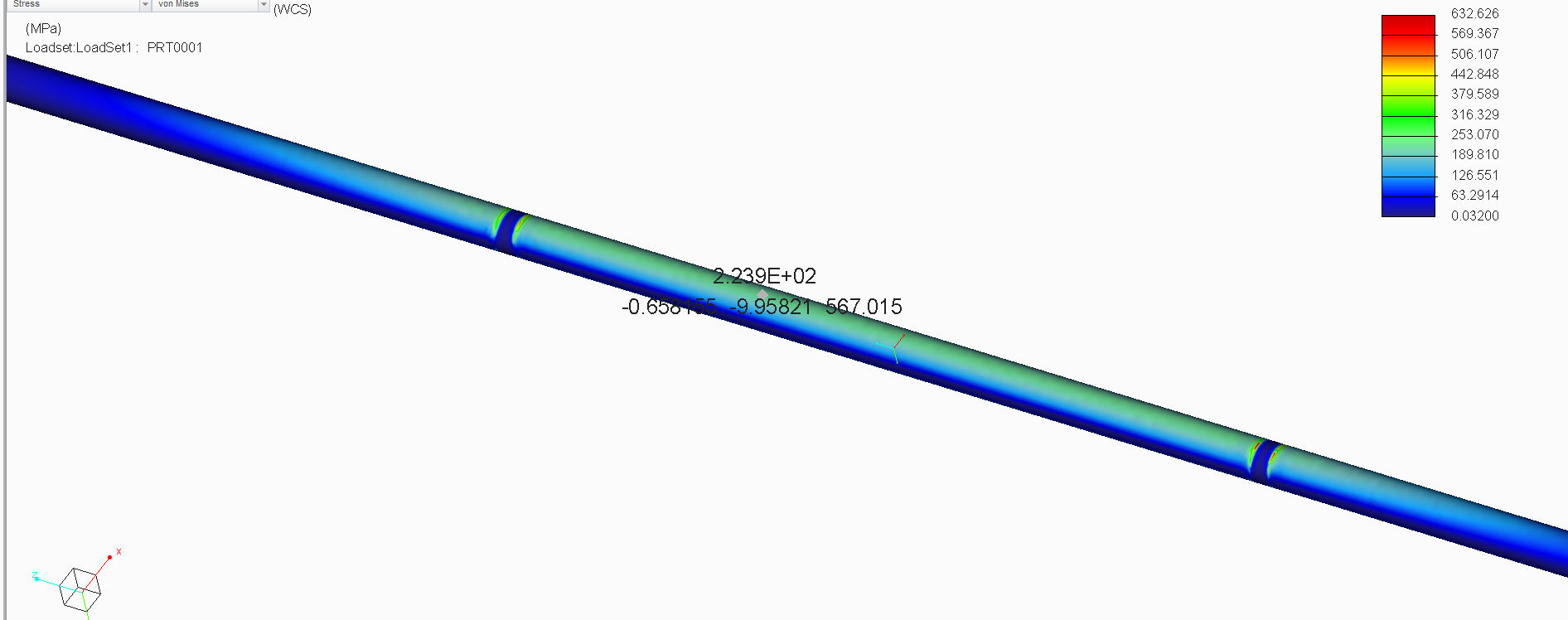
I have the structure in picture. The material of the beam is steel S235.
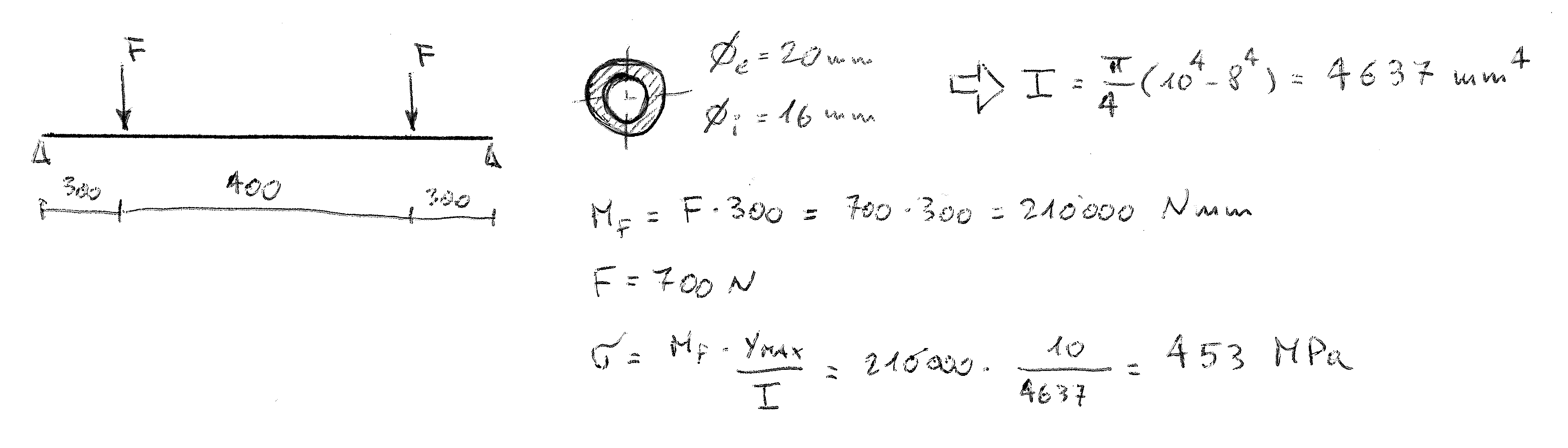
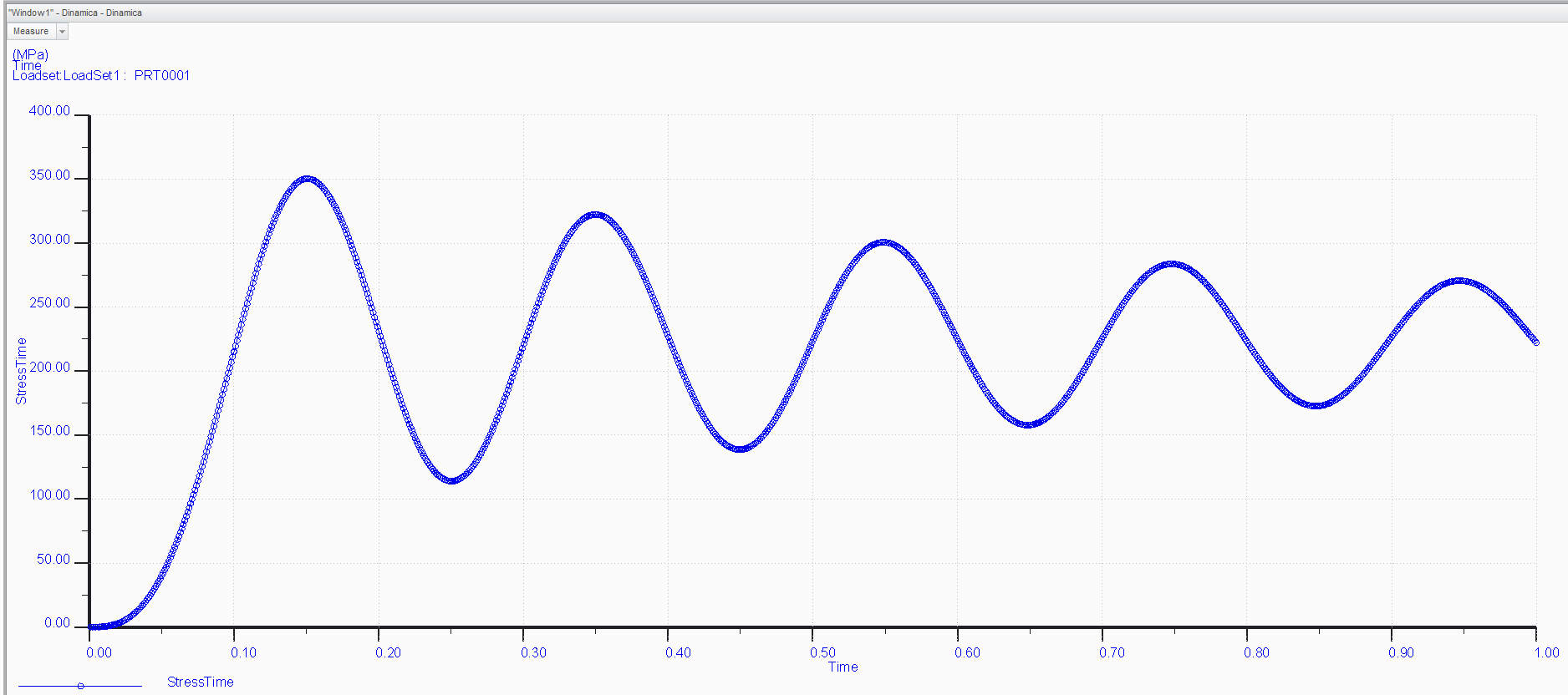
The real F is 350N, but I continuosly put and remove the load, so I take into account 2*F (found by match the elastic and potential energy, 0.5*k*x^2 = m*g*x).
I found a stress of 453 MPa, so this beam couldn't carry the load.
My question is, I'm using this beam every day, and it's not broken, nor bend.
Why it resist?
What is wrong in my calculation?
Thanks
I have the structure in picture. The material of the beam is steel S235.
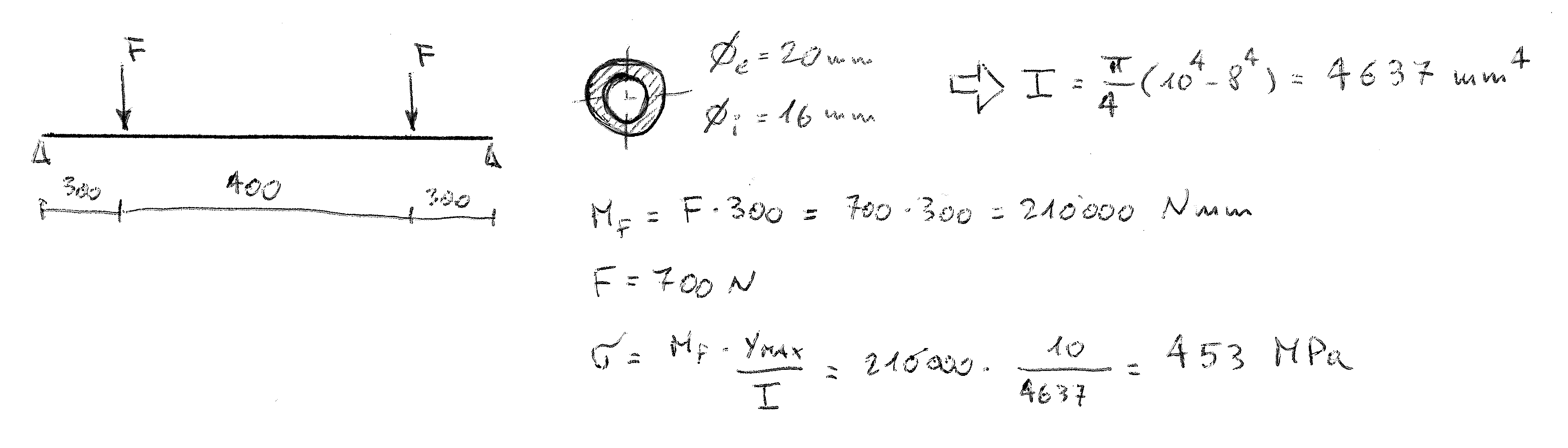
The real F is 350N, but I continuosly put and remove the load, so I take into account 2*F (found by match the elastic and potential energy, 0.5*k*x^2 = m*g*x).
I found a stress of 453 MPa, so this beam couldn't carry the load.
My question is, I'm using this beam every day, and it's not broken, nor bend.
Why it resist?
What is wrong in my calculation?
Thanks